ЭЛЕКТРОМАГНЕТИЗМ

Лекция №19

Опыты Эрстеда, Био и Савара, Ампера наглядно показали, что источником магнитного поля и объектом его воздействия являются электрические токи. Для количественного описания магнитного поля необходимо указать способ определение основной характеристики этого поля – индукции магнитного поля. В электростатике количественные характеристики поля определялись на основании поведения пробного точечного заряда в этом поле. В данном случае в качестве аналога пробного заряда удобнее всего использовать плоский контур с током.

Контур с током в магнитном поле. Индукция магнитного поля. Поместим контур с током между полюсами постоянного магнита и определим момент сил, действующий на контур при пропускании тока по нему, по величине угла закручивания пружины, соединенной с контуром:

- угол закручивания пружины пропорционален силе тока в контуре M~I;

- при неизменной силе тока угол закручивания пружины пропорционален площади контура M~S

M~ I ·S

Отсюда и появляется характеристика контура – его магнитный момент: p_m=I·S

Величина момента сил, действующая на контур с током при p_m const, пропорциональна синусу угла между направлением поля и нормалью к площадке, ограниченной контуром с током

M~ I· S· sin j

M_max~ I· S и тогда M_max / I· S не зависит от свойств контура и является основой количественной характеристики магнитного поля. M_max=р_m·В,

где В – индукция магнитного поля: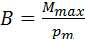

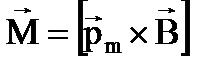Индукция магнитного поля – это векторная, силовая характеристика поля, равная отношению максимального момента сил, действующего на пробный контур с током, к магнитному моменту этого контура.

В векторной форме

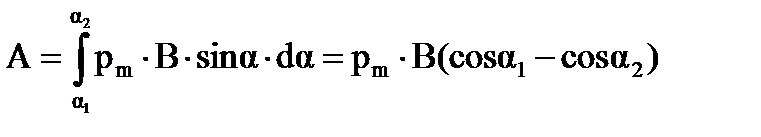Работа поворота контура с током в магнитном поле

Сила, действующая на проводник с током в магнитном поле (Сила Ампера) Если считать, что магнетизм обусловлен магнитными массами, то характер взаимодействия этих масс в точности повторяет закон взаимодействия точечных зарядов в электростатике (сила взаимодействия электрических и магнитных зарядов направлена по полю). Однако, ситуация изменяется кардинальным образом, если считать, что магнитное поле создается проводниками с током: если поместить проводник с током в магнитное поле, то сила, действующая на проводник направлена не по полю, а перпендикулярно ему.

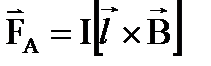Для определения величины силы, действующей на проводник с током со стороны магнитного поля, следует поместить прямоугольный контур с током в однородное магнитное поле, откуда

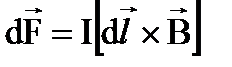Направление силы Ампера определяется по правилу буравчика: силовые линии поля входят в ладонь, четыре пальца показывают направление тока. Тогда отогнутый большой палец укажет направление силы.

В дифференциальной форме

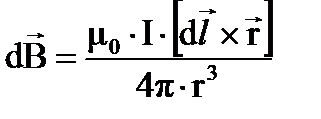Закон Био-Савара-Лапласа. Лаплас, анализируя результаты экспериментов Био и Савара, предложил способ отыскания величины индукции магнитного поля, создаваемого отрезками проводников с током произвольной конфигурации: для определения величины В необходимо разбить проводник на малые, элементарные участки dl и затем найти векторную сумму элементарных индукций dB, создаваемых всеми участками проводника.

Индукция магнитного поля в центре кругового тока: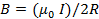

Индукция магнитного поля, создаваемая прямым проводником с током:

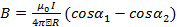
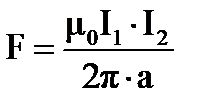Магнитное взаимодействие параллельных токов.

Один ток – источник магнитного поля, второй –

объект его воздействия.

F- сила, действующая на единицу длины одного проводника, со стороны магнитного поля, создаваемого всем другим проводником.

.

Из этого выражения следует определение единицы измерения силы тока: Один ампер - это сила постоянного тока, текущего по каждому из двух параллельных, бесконечно длинных проводников бесконечно малого кругового сечения в вакууме на расстоянии 1 метр, и создающая силу взаимодействия между ними 2×10⁻⁷ Н на каждый метр длины проводника.

Лекция №20

Теорема о циркуляции вектора В. Циркуляция вектора В магнитного поля, создаваемого прямым проводником с током I, по окружности радиуса R

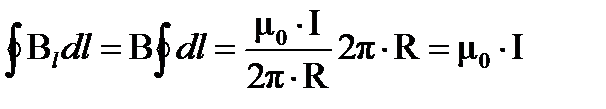
Оказывается, что этот результат справедлив и для случая проводника с током и замкнутого контура интегрирования произвольных форм. Используя принцип суперпозиции: Циркуляция вектора магнитной индукции равна алгебраической сумме токов, охватываемых контуром интегрирования, умноженной на μ₀.

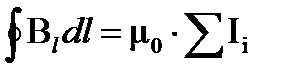
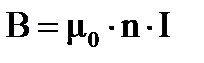Поле бесконечно длинного соленоида

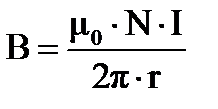Поле тороида

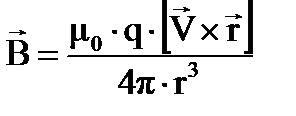Магнитное поле, создаваемое движущимся зарядом. Следуя историческому развитию магнетизма, найдем выражение для индукции магнитного поля, создаваемого движущимся зарядом, опираясь на закон Био-Савара-Лапласа – выражение для индукции магнитного поля, создаваемого элементом тока Idl

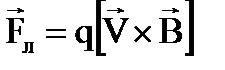Сила, действующая на движущийся заряд в магнитном поле (Сила Лоренца). Для получения выражения для силы, которая действует на движущийся заряд в магнитном поле, воспользуемся выражением для силы Ампера в дифференциальной форме и аналогией между элементом тока зарядом q, движущимся со скоростью V: Idl ↔qV

Движение заряда в магнитном поле:

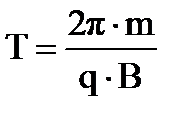V ||B – сила Лоренца равна нулю

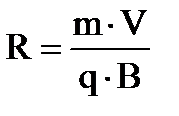
V B движение по окружности

В общем случае заряженная частица движется по винтовой линии

ЛЕКЦИЯ №21

Явление электромагнитной индукции. Основная идея: как с помощью магнитного поля

получить электрический ток?

Исторический экскурс. Неудачные опыты Колладона, выдающийся вклад Д. Генри в изучение явления электромагнитной индукции, эксперименты Фарадея с двумя изолированными друг от друга обмотками, намотанными на деревянный цилиндр, намотанными на тороидальный сердечник, магнитом, вдвигаемым в катушку, замкнутую на гальванометр.

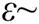Дополнительные эксперименты с катушкой, извлекаемой из пространства между полюсами магнита, показали, что сигнал, регистрируемый осциллографом, зависит от скорости «выдергивания» катушки, числа витков катушки, площади одного витка. ЭДС индукции, возникающая в проводящем контуре в изменяющемся магнитном поле пропорциональна скорости изменения магнитного потока и числу витков контура N:

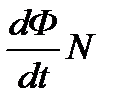
Вывод выражения для ЭДС индукции.

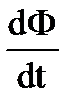
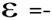Двухпроводная линия, короткозамкнутая с одной стороны, находится в однородном магнитном поле. Вдоль линии перемещается перемычка с постоянной скоростью V. На свободные заряды в движущейся перемычке действует сила Лоренца, которая «выталкивает» эти заряды из перемычки, приводя к возникновению тока в замкнутой цепи. Из сравнения выражения для сил, действующих на заряд, в магнитном и электрическом полях следует: B·V→ E, откуда

Правило Ленца: Индукционный ток всегда направлен так, чтобы противодействовать причине его вызывающей.

Потокосцепление или полный магнитный поток. Результирующий магнитный поток, пронизывающий контур, равен сумме потоков, пронизывающих каждый из витков.

Лекция №22

Потокосцепление или полный магнитный поток. Результирующий магнитный поток, пронизывающий контур, равен сумме потоков, пронизывающих каждый из витков.

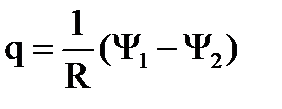Количество электричества, протекающее по замкнутому контуру, при изменении магнитного потока, пронизывающего этот контур

Это соотношение является основой для

измерения магнитных величин электрическими методами. Величина заряда q, протекающего по замкнутому контуру, определяется с помощью баллистического гальванометра.

ЯВЛЕНИЕ ВЗАИМНОЙ ИНДУКЦИИ. При пропускании тока по одному контуру возникает магнитный поток, часть которого пронизывает другой контур. Это явление носит название взаимной индукции.

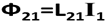Коэффициент взаимной индукции L_ik Элемент тока первого контураI₁dl₁ на элементарной площадке второго контура dS₂, создает элементарную индукцию dB, определяемую по закону Био-Савара-Лапласа. Интегрирование по первому контуру определяет величину индукции магнитного поля на площадке dS₂. Произведение нормальной компоненты вектора В на dS₂ определяет элементарный поток вектора dФ. Интегрирование по поверхности, ограниченной вторым контуром определяет величину потока индукции магнитного поля через поверхность S₂. Величина силы тока I₁ может быть вынесена за знаки обоих интегралов.

Статическое определение коэффициента взаимной индукции:

Коэффициент взаимной индукции – это физическая величина, связыващая магнитный поток, пронизывающий второй контур, с силой тока в первом контуре. Он зависит от геометрии контуров и их взаиморасположения. Численно коэффициент взаимной индукции равен магнитному потоку, пронизывающему второй контур, при силе тока в первом контуре, равной единице.

Динамическое определение коэффициента взаимной индукции: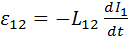

Коэффициент взаимной индукции – это физическая величина, связывающая ЭДС индукции, возникающую во втором контуре, со скоростью изменения силы тока в первом контуре. Он зависит от геометрии контуров и их взаиморасположения. Численно коэффициент взаимной индукции равен ЭДС индукции при скорости изменения силы тока в первом контуре на единицу в единицу времени.

ЯВЛЕНИЕ САМОИНДУКЦИИ: изменение тока в самом контуре приводит к изменению магнитного потока, пронизывающий данный контур и, следовательно, возникновению ЭДС индукции.

По аналогии со взаимной индукцией: Ф=LI

Статическое определение коэффициента самоиндукции: Коэффициент самоиндукции или индуктивность – это физическая величина, связывающая магнитный поток, пронизывающий данный контур, с силой тока в нем. Он зависит от геометрии контура. Численно коэффициент самоиндукции равен магнитному потоку, пронизывающему контур, при силе тока в нем, равной единице.

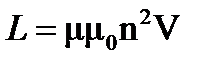Динамическое определение коэффициента самоиндукции: Коэффициент самоиндукции или индуктивность – это физическая величина, связывающая ЭДС индукции, возникающую в контуре, со скоростью изменения силы тока в нем. Он зависит от геометрии контура. Численно коэффициент самоиндукции равен ЭДС индукции при скорости изменения силы тока в контуре на единицу в единицу времени.

Индуктивность длинного соленоида

Включение и выключение цепи, содержащей катушку индуктивности

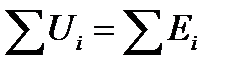
Экстра ток замыкания. Согласно второму закону Кирхгофа:

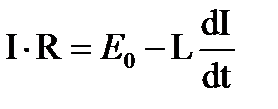
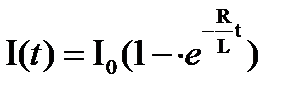
Экстра ток размыкания. После разделения переменных величин и интегрирования

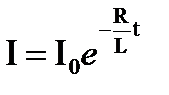
ЛЕКЦИЯ №23

Энергия магнитного поля тока. На цепочку, состоящую из катушки индуктивности L и сопротивления R, подаются прямоугольные импульсы напряжения. Из-за наличия катушки индуктивности ток не сразу достигает максимального значения, и не сразу становится равным нулю при U=0.

Объяснение этого эффекта - часть энергии, потребляемой от источника прямоугольных импульсов, тратится на создание магнитного поля катушки L, а при U=0 энергия магнитного поля катушки L превращается в Ленц-Джоулево тепло.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ПЛОТНОСТЬ ЭНЕРГИИ.

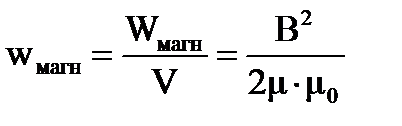
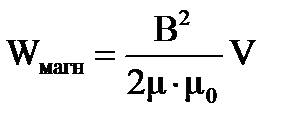
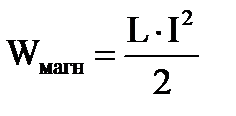Энергия, связанная с пропусканием тока по соленоиду, – это энергия магнитного поля внутри соленоида.

Магнитное поле в веществе Феноменологическое описание

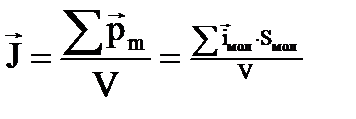Ампер выдвинул гипотезу о существовании молекулярных токов. Вектор намагничивания J или магнитный момент единицы объема:

Теорема о циркуляции вектора В

при наличии магнетика:

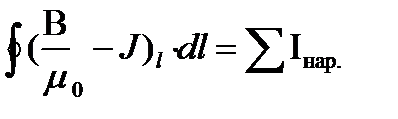
Учет количества молекулярных токов на элементе

контура интегрирования dl

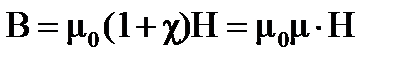
Связь индукции с напряженностью поля H:

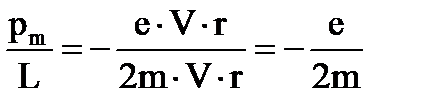Магнитные свойства электрона, атома, вещества

Магнитный момент электрона. Гиромагнитное отношение

Магнитный момент атомов. Опыт Штерна-Герлаха: ленточный пучок атомов пропускался через неоднородное магнитное поле. Оказалось, что атомы могут ориентироваться в магнитном поле только в строго определенных направлениях, причем число этих направлений различно для различных атомов.

Помимо магнитного момента, связанного с движением по круговой орбите, у электрона имеется собственный магнитный момент, который был назван спином.

Первоначально считалось, что спин обусловлен вращением электрона, как шарика, вокруг собственной оси. В дальнейшем, от этой наглядной картины пришлось отказаться.

Магнитные свойства вещества

ДИАМАГНЕТИКИ. Диамагнетизм обусловлен возникновением прецессии электронных орбит вокруг направления магнитного поля. Наведенный при этом магнитный момент направлен против внешнего поля. Диамагнетизм присущ всем веществам.

ПАРАМАГНЕТИКИ. Если магнитный момент атома или молекулы отличен от нуля, то, наряду с диамагнитным эффектом, проявляется ориентирующее действие магнитного поля. Тепловое хаотическое движение мешает ориентирующему действию поля, поэтому величина χ_р зависит от температуры.

ФЕРРОМАГНЕТИКИ. Существует особый класс веществ, магнитные свойства которых резко отличаются от диа и пара магнетиков. Это ферромагнетики. Аномально высокие значения χ для ферромагнетиков объясняются образованием доменов – областей спонтанного намагничивания, в которых собственные магнитные моменты (спины) ориентированы в одном и том же направлении. Во внешнем магнитном поле происходит перестройка доменной структуры: одни домены разворачиваются по направлению поля, домены изначально ориентированные вдоль поля разрастаются за счет доменов с противоположной ориентацией. На зависимости В(Н) возникает гистерезис. При температуре Кюри доменная структура разрушается, и ферромагнетик превращается в парамагнетик. При понижении температуры вещество возвращается в ферромагнитное состояние На зависимости В(Н) возникает гистерезис.

ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В проводящем контуре, помещенном в изменяющееся магнитное поле, возникает ЭДС индукции. Идея Максвелла: проводящий контур является лишь индикатором вихревого электрического поля, возникающего вокруг изменяющегося магнитного поля.

Различия между линиями электростатического и вихревого поля. Силовые линии электростатического поля не являются замкнутыми. Они начинаются на + и оканчиваются на – зарядах.Силовые линии вихревого электрического поля являются замкнутыми. Электростатическое поле обладает свойством потенциальности: работа электрического поля по перемещению заряда по замкнутому контуру в этом поле равна нулю.

Вихревое электрическое поле не является потенциальным: работа электрического поля по перемещению заряда по замкнутому контуру в этом поле не равна нулю.

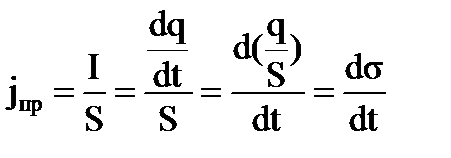ТОК СМЕЩЕНИЯ Схема: источник питания, тумблер, конденсатор и лампочка. С помощью тумблера периодически изменяется полярность напряжения, подаваемого на конденсатор. При этом лампочка горит непрерывно. Линии тока обрываются на пластинах конденсатора. Для восстановления непрерывности линий тока Максвелл предложил считать, что на пластинах конденсатора линии тока проводимости переходят в линии тока смещения между обкладками конденсатора.

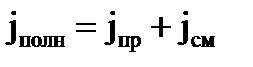
Вектор полного тока:

С одной стороны ток смещения – это абстракция. Его прохождение не связано с выделением Ленц-Джоулева тепла. Однако, вокруг тока смещения образуется вихревое магнитное поле.

УРАВНЕНИЯ МАКСВЕЛЛА В ИНТЕГРАЛЬНОЙ ФОРМЕ

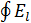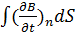
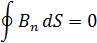
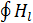dl=-

dl= +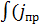

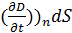
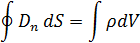
j=sE

D=ee₀E

B=mm₀H

Дата добавления: 2014-11-24; просмотров: 424; Нарушение авторских прав

Мы поможем в написании ваших работ!