
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Прямые методы оптимизации функции одной переменной
на тему: “Прямые методы оптимизации функции одной переменной”
Работу выполнили:
студентки группы АСПМ 11-1 Царева М.А.,
Давыдова Д.Н.
Работу проверил:
преподаватель Мазуров А.Ю.
Арзамас, 2013 г
Задача 1:
Минимизировать функцию f(x)=x(x-1)2 на отрезке [0,5;2] методом парабол.
Листинг программы:
clc
close all
clear all
a=0.5;
b=2;
x1=0.75;
x2=1;
x3=1.25;
y1=x1*(x1-1)^2;
y2=x2*(x2-1)^2;
y3=x3*(x3-1)^2;
A=y1/((x1-x3)*(x1-x2))+ y2/((x2-x3)*(x2-x1))+y3/((x3-x1)*(x3-x2))
B=y1*(x2+x3)/((x1-x2)*(x3-x1))+y2*(x1+x3)/((x2-x1)*(x3-x1))+y3*(x2+x1)/((x2-x3)*(x3-x1))
C=y1*x2*x3/((x1-x2)*(x1-x3))+y2*x1*x3/((x2-x1)*(x2-x3))+y3*x2*x1/((x3-x2)*(x3-x1))
X=-B/(2*A)
F=A*X^2+B*X+C;
x=0.5:0.01:2;
y=x.*(x-1).^2;
f=A*x.^2+B.*x+C;
plot(x,y,'k');
hold on;
plot(x,f,'r');
Результат работы программы:
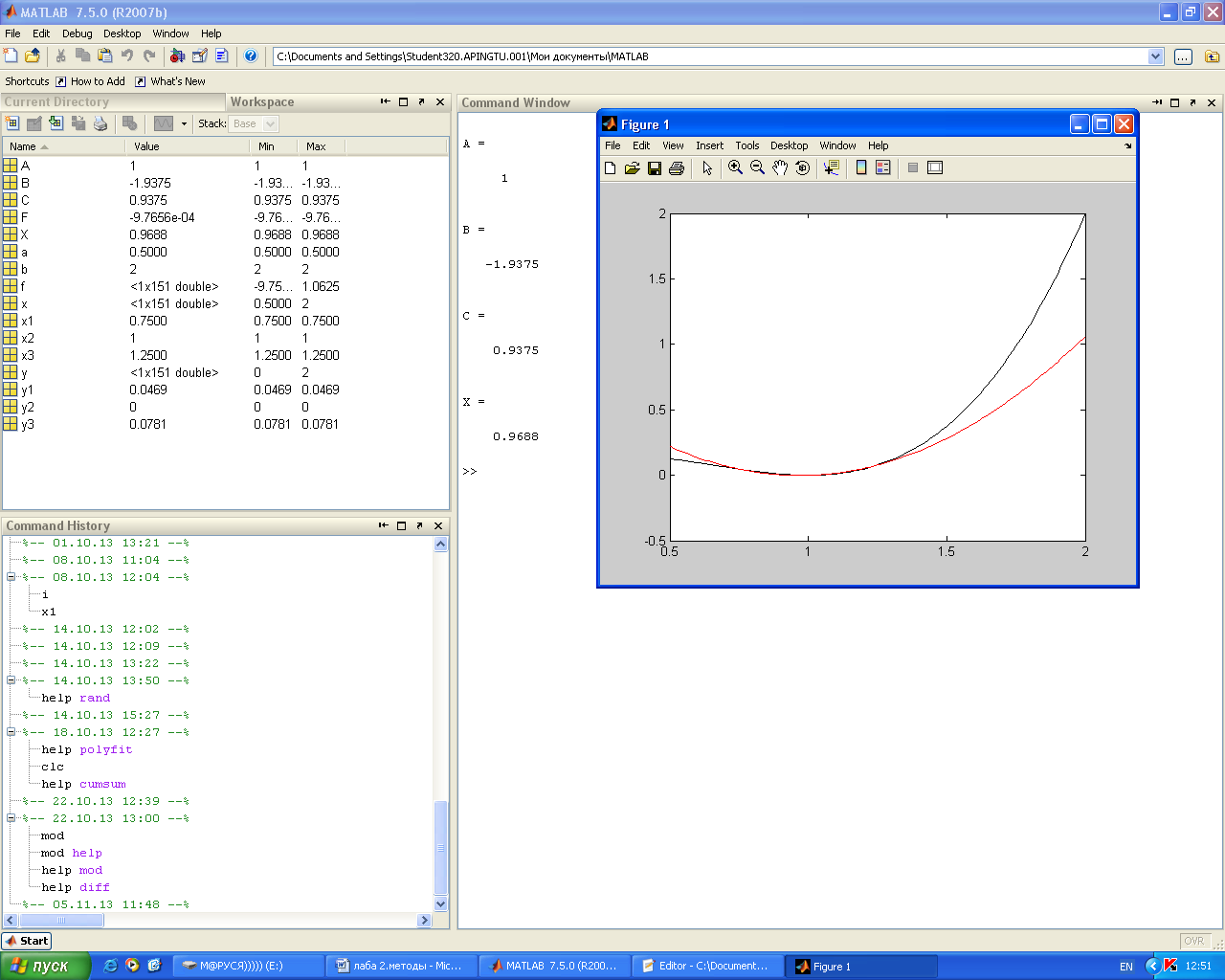
Задача 2:
Минимизировать функцию f(x)=x/(x^2+1) на отрезке [-1;0.75] методом средней точки.
Листинг программы:
%Вторая задача
a=-3;
b=0.75;
e=0.001;
syms x;
df=diff(x/(x^2+1))
xmin=(a+b)/2;
while (abs((1/(xmin^2+1)-2*xmin^2/(xmin^2+1)^2))<e)
if (1/(xmin^2+1)-2*xmin^2/(xmin^2+1)^2)>0 b=xmin; xmin=(a+b)/2;
else a=xmin; xmin=(a+b)/2;
end
end
ymin=xmin/(xmin^2+1)
xmin
fplot('x/(x^2+1)',[-3 0.75])
Результат работы программы:
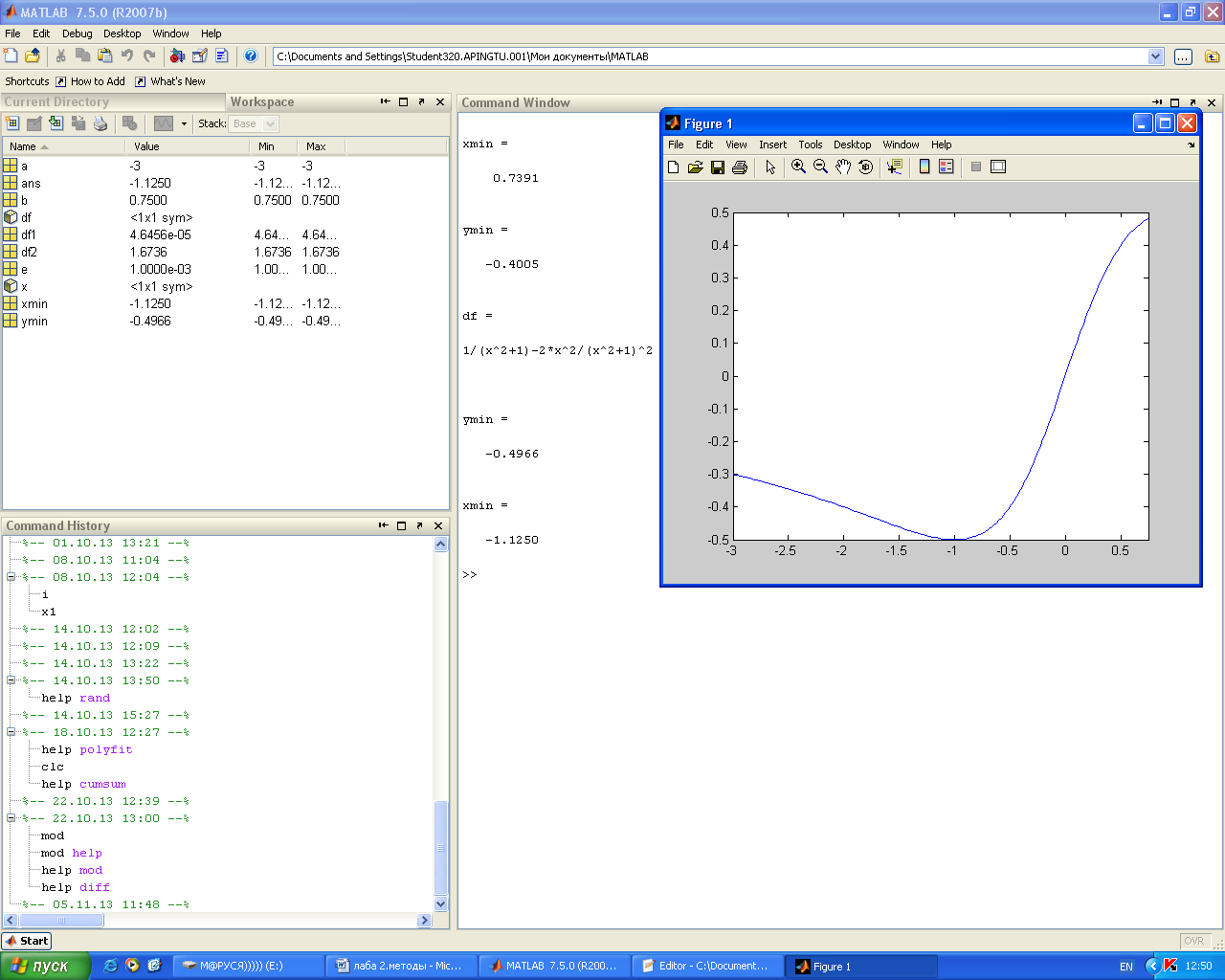
Задача 3:
Минимизировать функцию f(x)=-exp(-x)*sh(x/2) на отрезке [-1;3] методом хорд.
Листинг программы:
%Третья задача
clc
close all
clear all
a=-1;
b=3;
e=0.001;
df1=exp(-a)*sinh(1/2*a)-1/2*exp(-a)*cosh(1/2*a)
df2=exp(-b)*sinh(1/2*b)-1/2*exp(-b)*cosh(1/2*b)
X=-((df1*(b-a))/(df2-df1))+a;
f=exp(-X)*sinh(1/2*X)-1/2*exp(-X)*cosh(1/2*X);
while(abs(f)>e)
if (f<0) a=X;
else b=X;
end
X=-((df1*(b-a))/(df2-df1))+a;
f=exp(-X)*sinh(1/2*X)-1/2*exp(-X)*cosh(1/2*X);
end
fplot('-exp(-x)*sinh(x/2)',[-1 3])
xmin=(a+b)/2
ymin=-exp(-xmin)*sinh(xmin/2)
Результат работы программы:

Задача 4:
Минимизировать функцию f(x)=1/2*x^2-sin(x) на отрезке [0;2] методом Ньютона.
Листинг программы:
clc
close all
clear all
a=0;
b=2;
e=0.001;
x=(a+b)/2;
df1=x-cos(x);
df2=1+sin(x);
while (abs(df1)>=e)
x=x-(df1/df2);
df1=x-cos(x);
df2=1+sin(x);
end
xmin=x
ymin=1/2*x^2-sin(x)
fplot('1/2*x^2-sin(x)',[0 2])
Результат работы программы:
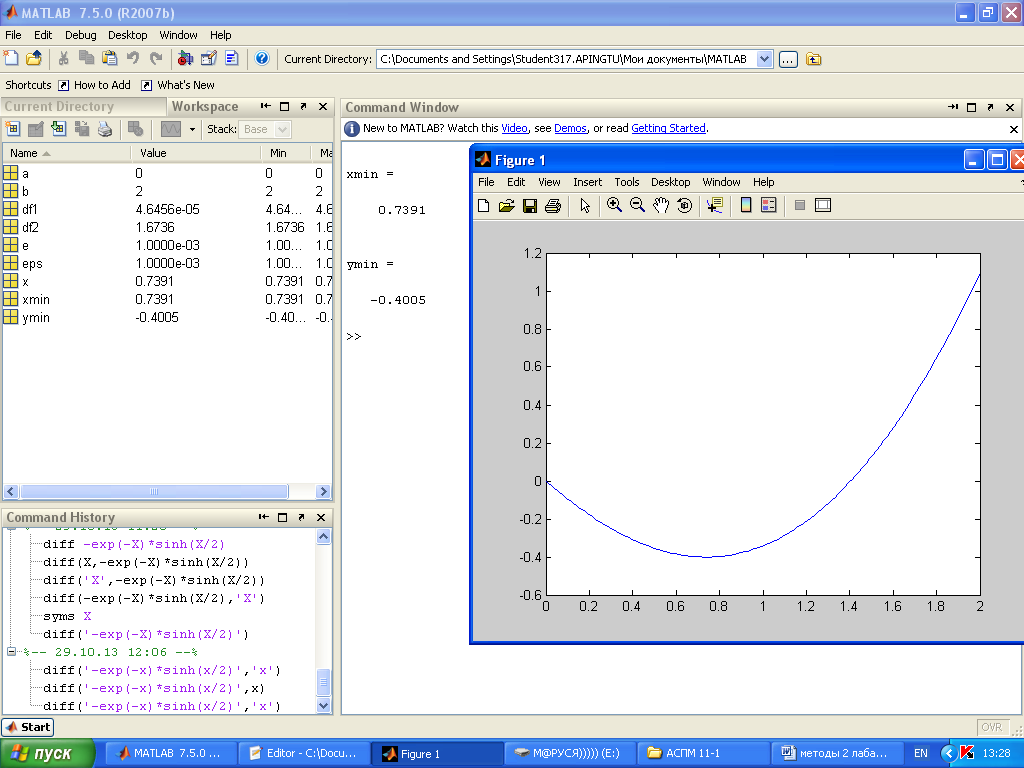
| <== предыдущая страница | | | следующая страница ==> |
| Расчет срока окупаемости с учетом дисконтирования для четвертого проекта | | |
Дата добавления: 2014-11-24; просмотров: 298; Нарушение авторских прав

Мы поможем в написании ваших работ!