
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Формула Стокса
Эта формула позволяет преобразовать криволинейный интеграл вдоль замкнутой пространственной кривой в поверхностный интеграл по поверхности, натянутой на эту кривую,
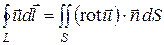 ,
,
т.е. циркуляция вектора поля вдоль контура равна потоку вихря через поверхность, ограниченную этим контуром.
4.4.4. Формула Гаусса-Остроградского.
Это соотношение, часто называемое преобразованием Гаусса-Остроградского, связывает поверхностный интеграл по замкнутой поверхности с тройным интегралом по области, ограниченной этой поверхностью,
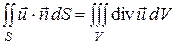 .
.
Эта зависимость показывает, что поток векторного поля через замкнутую поверхность равен тройному интегралу от дивергенции поля по объему, ограниченному этой поверхностью.
В механике жидкости широко используется формула, являющаяся следствием формулы Гаусса-Остроградского для скалярного поля
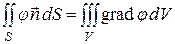 ,
,
где j - скалярная функция.
4.5. ТЕНЗОР НАПРЯЖЕНИЯ.
Для уяснения дальнейшего материала рассмотрим более подробно, например, вектор 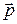 . С этой целью выделим в движущейся жидкости частицу в виде тетраэдра (рис. 4.2).
. С этой целью выделим в движущейся жидкости частицу в виде тетраэдра (рис. 4.2).
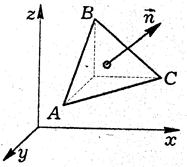 Рисунок 4.2 - К определению тензора напряжений
Рисунок 4.2 - К определению тензора напряжений
Пусть 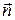 - внешняя нормаль к четвертой (наклонной) грани тетраэдра, а площадь этой грани обозначим
- внешняя нормаль к четвертой (наклонной) грани тетраэдра, а площадь этой грани обозначим 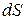 . Площади остальных граней – соответственно
. Площади остальных граней – соответственно 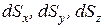 , которые можно рассматривать как проекции грани АВС на соответствующие оси координат.
, которые можно рассматривать как проекции грани АВС на соответствующие оси координат.
Тогда
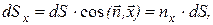
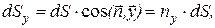
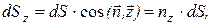
где  - направляющие косинусы.
- направляющие косинусы.
Обозначим объем тетраэдра 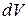 , тогда действующая на него массовая сила будет
, тогда действующая на него массовая сила будет 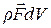 , а массовая сила инерции -
, а массовая сила инерции - 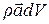 , где
, где 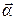 – вектор ускорения тетраэдра.
– вектор ускорения тетраэдра.
Поверхностная сила, действующая на наклонную часть, 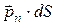 . Для остальных трех граней
. Для остальных трех граней
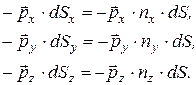
Знаки «минус» свидетельствуют о том, что векторы 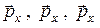 направлены в стороны, противоположные координатным осям.
направлены в стороны, противоположные координатным осям.
Запишем уравнение движения тетраэдра, которое в соответствии с законом движения механики, имеет вид
Масса 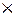 ускорение = результирующая массовых сил +
ускорение = результирующая массовых сил +
+ результирующая поверхностных сил,
т.е.
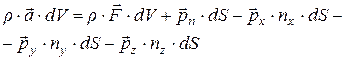 .
.
Величины 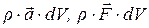 являются второго порядка малости, поэтому можно записать
являются второго порядка малости, поэтому можно записать
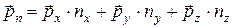 .
.
Из этого равенства следует, что напряжение 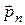 при произвольной ориентации нормали может быть определено, если известны напряжения в этой же точке для площадок, внешние нормали которых параллельны осям координат.
при произвольной ориентации нормали может быть определено, если известны напряжения в этой же точке для площадок, внешние нормали которых параллельны осям координат.
Проекции векторов 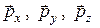 на координатные оси будем обозначать
на координатные оси будем обозначать
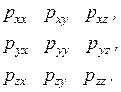
В этом обозначении первый подстрочный индекс указывает ось, перпендикулярную ориентации площадки, второй индекс – ось, на которую спроектировано напряжение.
Для уяснения сказанного выше рассмотрим параллелепипед, выделенный в движущейся жидкости (рис. 4.3).
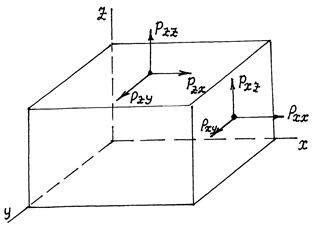
Рисунок 4.3 - К определению двойных индексов напряжений
Из рисунка видно, что напряжения с одинаковыми индексами являются нормальными, а с разными индексами – касательными к площадкам параллелепипеда.
Приведенное выше выражение движения тетраэдра
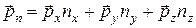
в принятых нами обозначениях напряжений с двойными индексами будет иметь вид
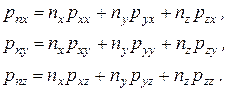
Совокупность этих девяти составляющих компонентов напряжения образуют тензор напряжения. В матричной форме он запишется в виде
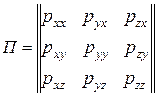 .
.
Доказано, что тензор напряжения является симметричным. Это означает, что величины, расположенные симметрично главной диагонали, равны, т.е.
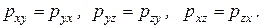
Откуда следует, что для нахождения тензора напряжений достаточно знать не девять, как указывалось выше, а шесть скалярных величин.
К понятию тензора можно подойти и другим путем. Представим тензор как оператор, с помощью которого можно преобразовать вектор в вектор или векторы в векторы. На основании этого можем записать
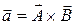 ,
,
где 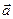 - выходной вектор,
- выходной вектор, 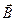 - входной вектор,
- входной вектор, 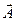 - оператор, который и наз. тензором.
- оператор, который и наз. тензором.
Существенным ограничением является то, что оператор должен быть линейным.
Таким образом, определить тензор – это означает задать закон (правило), по которому один вектор преобразуется в другой вектор.
Вязкость жидкости не проявляется, если она находится в состоянии равновесия, т.е. в этом случае касательные компоненты тензора равны нулю и действуют лишь нормальные 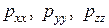 , ориентированные по внешним нормалям (рис. 4.3). Они являются растягивающими напряжениями. Жидкое тело способно воспринимать лишь сжимающие усилия. Можно показать, что при отсутствии касательных напряжений
, ориентированные по внешним нормалям (рис. 4.3). Они являются растягивающими напряжениями. Жидкое тело способно воспринимать лишь сжимающие усилия. Можно показать, что при отсутствии касательных напряжений 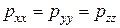 , из чего следует, что нормальные напряжения в данной точке не зависят от ориентации площадки. Величины, численно равные нормальным напряжениям, но взятые с противоположным знаком, в гидромеханике называют давлением, либо более полно – гидростатическим давлением. Гидростатическое давление обозначают буквой р, т.е.
, из чего следует, что нормальные напряжения в данной точке не зависят от ориентации площадки. Величины, численно равные нормальным напряжениям, но взятые с противоположным знаком, в гидромеханике называют давлением, либо более полно – гидростатическим давлением. Гидростатическое давление обозначают буквой р, т.е.
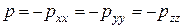 .
.
Т.о., гидростатическое давление, являясь скалярной величиной (как компонента тензора), не зависит от ориентации площадки, на которую оно действует.
5. УРАВНЕНИЕ ДВИЖЕНИЯ ЖИДКОСТИ В НАПРЯЖЕНИЯХ.
Проанализируем движения жидкой частицы, масса которой 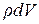 и поверхность
и поверхность 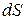 .
.
Уравнение движения имеет вид
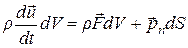 .
.
Для движущегося объема V, поверхность которого S, имеем
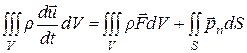
Преобразуем поверхностный интеграл в объемный с учетом того, что тензор напряжений имеет вид
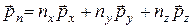 ,
,
где 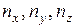 – направляющие косинусы.
– направляющие косинусы.
Воспользовавшись известным из векторного анализа соотношением
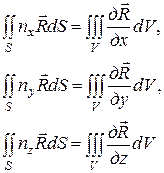
применительно к тензору напряжений 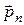 , получим
, получим
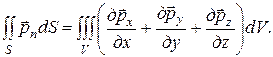
Подставив это выражение в исходное уравнение, получим
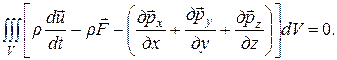
Но т.к. объем выбран произвольно и dV¹ 0, получим
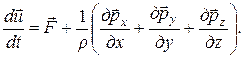
Это и есть уравнение движения жидкости в напряжениях.
В проекциях на декартовы оси координат это выражение примет вид
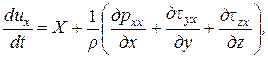
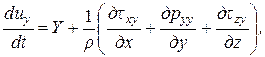
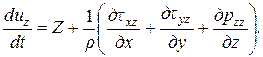
Эта система включает девять неизвестных величин – три проекции скорости и шесть проекций напряжений. Проекции единичных массовых сил, как правило, известны из постановки задачи.
| <== предыдущая страница | | | следующая страница ==> |
| Циркуляция вектора поля | | | Значение туризма |
Дата добавления: 2014-12-09; просмотров: 283; Нарушение авторских прав

Мы поможем в написании ваших работ!