
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Составление линейных математических моделей
Задача линейного программирования является достаточно распространенной задачей принятия оптимальных решений в производственном менеджменте. Общая задача линейного программирования (ОЗЛП) математически может быть сформулирована следующим образом:
Найти значения переменных X1, X2, ..., Xn, максимизирующих (минимизирующих) линейную форму
F ( 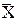 )
)  = c1 * X1 + c2 * X2 + ... + cn * Xn (1)
= c1 * X1 + c2 * X2 + ... + cn * Xn (1)
при условиях
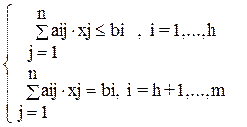 , (2-3)
, (2-3)
xj 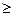 0, j = 1,...,p , (p
0, j = 1,...,p , (p 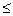 n) . (4)
n) . (4)
Соотношения (2-3) называются функциональными ограничениями, а (4) – прямыми.
Пример 1. Металлургическому заводу требуется уголь с содержанием фосфора не более 0.03% и с долей зольных примесей не более 3.25%. Завод закупает три сорта угля А, В, С с известным содержанием примесей. В какой пропорции нужно смешивать исходные продукты А, В, С, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену?
Содержание примесей и цена исходных продуктов приведены в табл. 1.
Таблица 1
| Сорт | Содержание (%) | Цена | |
| угля | фосфора | золы | 1 т, руб. |
| А В С | 0.06 0.04 0.02 | 2.0 4.0 3.0 |
Построим математическую модель.
Обозначим:
Х1 – количество угля сорта А в тонне смеси;
Х2 – количество угля сорта В в тонне смеси, (переменные);
Х3 – количество угля сорта С в тонне смеси.
F( 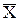 ) = 30×X1 + 30×X2 + 45×X3 - стоимость 1 т. смеси (целевая функция),
) = 30×X1 + 30×X2 + 45×X3 - стоимость 1 т. смеси (целевая функция),
0.06×Х1 + 0.04×Х2 + 0.02×Х3 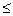 0.03 (%) - ограничение на содержание фосфора в смеси,
0.03 (%) - ограничение на содержание фосфора в смеси,
2×Х1 + 4×Х2+ 3×Х3 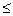 3.25 (%) - ограничение на содержание зольных примесей,
3.25 (%) - ограничение на содержание зольных примесей,
Х1+ Х2 + Х3 = 1 (т.) - ограничение на состав 1 т. смеси.
Окончательно, математическая модель имеет вид.
Определить количество угля сортов А, В, С (Х1, Х2, Х3) в тонне смеси, при которых достигается
F( 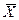 ) = 30×X1 + 30×X2 + 45×X3
) = 30×X1 + 30×X2 + 45×X3 
при ограничениях
0.06×Х1 + 0.04×Х2 + 0.02×Х3 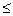 0.03
0.03
2×Х1 + 4×Х2 + 3×Х3 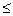 3.25
3.25
Х1 + Х2 + Х3 = 1
Х1,X2,X3 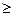 0.
0.
Пример 2. Бройлерное хозяйство птицеводческой фермы насчитывает 20 000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Недельный расход корма в среднем (за 8 недель) составляет 500г = 0.5 кг.
Для того, чтобы цыплята достигли к 8-й неделе необходимого веса, кормовой рацион должен удовлетворять определённым требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов.
В табл. 2 приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента. Смесь должна содержать:
¨ не менее 0.8% кальция;
¨ не менее 22% белка (от общего веса смеси);
¨ не более 5% клетчатки.
Требуется определить количество (в кг) каждого из трёх ингредиентов, образующих смесь минимальной стоимости, при соблюдении требований к общему расходу кормовой смеси и её питательности.
Таблица 2
| Ингредиент | Содержание питательных веществ (кг/ингредиента) | Стоимость (руб./кг) | ||
| Кальций | Белок | Клетчатка | ||
| Известняк Зерно Соевые бобы | 0.38 0.001 0.002 | - 0.09 0.50 | - 0.02 0.08 | 0.04 0.15 0.40 |
Математическая формулировка задачи.
Введём следующие обозначения:
Х1 - содержание известняка в смеси (кг);
Х2 - содержание зерна в смеси (кг);
Х3 - содержание соевых бобов в смеси (кг);
Общий вес смеси, еженедельно расходуемый на кормление цыплят:
20 000 * 0.5 = 10 000 кг.
Ограничения, связанные с содержанием кальция, белка и клетчатки в кормовом рационе, имеют вид:
0.38×Х1 + 0.001×Х2 + 0.002×Х3 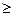 0.008 * 10 000,
0.008 * 10 000,
0.09×Х2 + 0.50×Х3 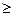 0.22 × 10 000,
0.22 × 10 000,
0.02×Х2 + 0.08×Х3 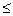 0.05 × 10 000.
0.05 × 10 000.
Окончательный вид математической формулировки задачи:
F( 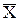 ) = 0.04×X1 + 0.15×X2 + 0.40×X3
) = 0.04×X1 + 0.15×X2 + 0.40×X3 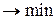
при ограничениях
Х1 + Х2 + Х3 = 10 000
0.38×Х1 + 0.001×Х2 + 0.002×Х3 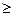 80
80
0.09×Х2 + 0.50×Х3 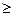 2200
2200
0.02×Х2 + 0.08×Х3 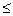 500
500
Хj 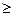 0, j = 1, 2, 3.
0, j = 1, 2, 3.
Пример 3. В отделе технического контроля (ОТК) некоторой фирмы работают контролеры разрядов 1 и 2. Норма выработки ОТК за 8-часовой рабочий день составляет не менее 1800 изделий. Контролер разряда 1 проверяет 25 изделий в час, причем не ошибается в 98% случаев. Контролер разряда 2 проверяет 15 изделий в час; его точность составляет 95%.
Заработная плата контролера разряда 1 равна 4 руб. в час, контролер разряда 2 получает 3 руб. в час. При каждой ошибке контролера фирма несет убыток в размере 2 рубля. Фирма может использовать 8 контролеров разряда 1 и 10 контролеров разряда 2. Руководство фирмы хочет определить оптимальный состав ОТК, при котором общие затраты на контроль будут минимальными.
Математическая формулировка задачи.
Пусть X1 и X2 обозначают количество контролеров разрядов 1 и 2 соответственно. Число контролеров каждого разряда ограничено, т.е. имеются следующие ограничения:
X1 £ 8 (разряд 1)
X2 £ 10 (разряд 2)
Ежедневно необходимо проверять не менее 1800 изделий. Поэтому выполняется неравенство
8×25×X1 + 8×15×X2 = 200×X1 + 120×X2 ³ 1800,
или 5×X1 + 3×X2 ³ 45.
При построении целевой функции следует иметь в виду, что расходы фирмы, связанные с контролем, включают две составляющие:
1) зарплату контролеров.
2) убытки, вызванные ошибками контролеров.
Расходы на одного контролера разряда 1 в час составляют
4 руб. + 2×25×0,02 руб. = 5 руб.
Расходы на одного контролера разряда 2 в час составляют
3 руб. + 2×15×0,05 руб. = 4 руб.50 коп.
Следовательно, минимизируемая целевая функция, выражающая ежедневные расходы на контроль, имеет вид
8×(5×X1 + 4,5×X2) = 40×X1 + 36×X2.
Теперь можно сформулировать следующую задачу ЛП
F( 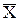 ) = 40×X1 + 36×X2
) = 40×X1 + 36×X2 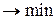
при ограничениях
X1 £ 8
X2 £ 10
5×X1 + 3×X2 ³ 45
X1,Х2 ³ 0 .
| <== предыдущая страница | | | следующая страница ==> |
| Решение задачи с помощью построенной модели | | | Основные термины и определения. Гидропривод включает насос и гидродвигатель с соответствующей аппаратурой (устройствами) управления |
Дата добавления: 2014-12-09; просмотров: 446; Нарушение авторских прав

Мы поможем в написании ваших работ!