Моделирование цепей Маркова

Рассмотрим пример технического устройства S состоящего из двух узлов, каждый из которых в случайный момент времени может выйти из строя (отказать), после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное, случайное время. Возможные состояния данной системы можно перечислить:

S₀ – оба узла исправны,

S₁ – первый узел ремонтируется, второй исправен,

S₂ – второй узел ремонтируется, первый исправен,

S₃ – оба узла ремонтируются.

Интенсивности потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу. Это будет именно так, если ремонтом каждого узла занят отдельный специалист.

При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой – так называемым графом состояний. Состояния системы изображаются прямоугольниками (или кругами), а возможные переходы из состояния в состояние – стрелками, соединяющими состояния.

Для рассмотренного примера граф состояния имеет вид, представленный на рис. 3.2. Стрелка, направленная из S₀ в S₁, означает переход в момент отказа первого узла; стрелка, направленная обратно, из S₁в S₀, – переход в момент окончания ремонта этого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа.

Рис. 3.2. Граф состояния

Рассмотрим простейший поток событий с интенсивностью λ и произвольный элементарный (очень маленький) участок времени Δt.

Элементом вероятности называется вероятность попадания на этот участок хотя бы одного события потока.

Элемент вероятности (с точностью до малых величин более высокого порядка по сравнению с Δt) равен

p_{Δt =} λ Δt ,

т.е. для простейшего потока элемент вероятности равен интенсивности потока, умноженной на длину элементарного участка.

Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии S₀. Какой поток событий переводит ее в состояние S₁? Очевидно, поток отказов первого узла. Его интенсивность λ₁ равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из S₁ в S₀? Очевидно, поток "окончаний ремонтов" первого узла. Его интенсивность μ₁ равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 3.2.

Если процесс, протекающий в системе с дискретными состояниями и непрерывным временем является марковским, то для вероятностей состояний p₁(t), ..., p_n(t) можно составить систему линейных дифференциальных уравнений. При составлении этих уравнений удобно пользоваться графом состояний системы, на котором против каждой стрелки, ведущей из состояния в состояние, проставлена интенсивность потока событий, переводящего систему по стрелке.

Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний p_i(t) как функции времени. Для этого составляются и решаются так называемые уравнения Колмогорова – особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний. Для этого составляются и решаются так называемые уравнения Колмогорова – особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний.

Сформулируем общее правило составления уравнений Колмогорова.

В левой части каждого из них стоит производная вероятности какого-то
(i-го) состояния. В правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го) состояния.

Пользуясь этим правилом, запишем уравнения Колмогорова для системы S, размеченный граф состояний которой дан на рис. 3.2:

(3.1)

Чтобы решить эту систему уравнений найти вероятности состояний, прежде всего надо задать начальные условия. Начальные условия отражают состояние системы в начальный момент времени. Если, например, система при t = 0 была в состоянии S_k, то p_k (0) = 1, p_i (0) = 0 при i = 1, n и i ≠ k. Эти уравнения можно решать аналитически, но это удобно только тогда, когда число уравнений не превышает двух (иногда трёх). В случае, когда уравнений оказывается больше, применяют численные методы.

Что будет происходить с вероятностями состояний при ? Будут ли p₁(t), ..., p_n(t) стремиться к каким-то пределам?

Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний: . p_i – среднее относительное время пребывания системы в i-ом состоянии.

В теории случайных процессов доказывается, что если число n состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое, то финальные вероятности существуют.

Финальную вероятность состояния S_i можно истолковать как среднее относи тельное время пребывания системы в этом состоянии.

Как найти финальные вероятности? Поскольку все p_i = const, то производные, стоящие в левой части каждого уравнения равны нулю. Таким образом, мы получили систему линейных алгебраических уравнений. Поскольку ни одно уравнение в этой системе не имеет свободного члена, то система является вырожденной (т.е. все переменные будут выражены через одну). Чтобы этот избежать, необходимо воспользоваться нормировочным условием ( 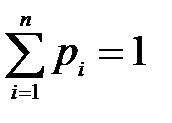), при этом любое из уравнений можно отбросить.

Для рассматриваемого примера из системы дифференциальных уравнений (3.1) получим:

(3.2)

Зададимся численными значениями интенсивностей

λ₁ = 1, λ₂ = 2, μ₁ = 2, μ₂ = 3

и решим систему (3.2). Пожертвуем четвертым уравнением, добавив вместо него нормировочное условие:

Решая эту систему алгебраических уравнений, получим:

р₀ = 0.4; р₁ = 0.2; р₂ ≈ 0.27; p₃ ≈ 0.13.

т.е. в предельном, стационарном режиме система S в среднем 40% времени будет проводить в состоянии S₀ (оба узла исправны), 20% – в состоянии S₁ (первый узел ремонтируется, второй работает), 27% – в состоянии S₂ (второй узел ремонтируется, первый работает) и 13% – в состоянии S₃ полной негодности (оба узла ремонтируются). Знание этих финальных вероятностей может помочь оценить среднюю эффективность работы системы и загрузку ремонтных органов.

Предположим, что система S в состоянии S₀ (полностью исправная) приносит в единицу времени доход 8 (условных единиц), в состоянии S₁– доход 3, в состоянии S₂– доход 5, в состоянии S₃– вообще не приносит дохода. Тогда в предельном, стационарном режиме средний доход в единицу времени будет

W = 0.4*8 + 0.2*3 + 0.27*5 = 5.15

Теперь оценим загрузку ремонтных органов (рабочих), занятых ремонтом узлов 1 и 2.

Узел 1 ремонтируется долю времени, равную р₁ + p₃= 0.2 + 0.13 = 0.33.

Узел 2 ремонтируется долю времени р₂ + p₃= 0.4.

Основные понятия систем массового обслуживания

Требованием или заявкой называется объект, который необходимо обслужить: железнодорожные составы, проходящие через железнодорожный узел, покупатели, приобретающие товар и т.д. Объект обычно является носителем запроса. Поэтому в дальнейшем под требованием понимается и сам запрос на обслуживание. Например, запрос на ремонт станка, запрос на продажу товара покупателю и т.д.

Поток требований – совокупность требований, поступающих в систему массового обслуживания.

Последовательность требований, входящих в систему массового обслуживания, называется входящим (входным) потоком, выходящие требования называются выходящим (выходным) потоком.

Устройства, удовлетворяющие запросу на обслуживание, называются обслуживающими устройствами (аппаратами, приборами).

Совокупность всех обслуживающих устройств называется цехом.

Канал – обслуживающее устройство в цехе, пропускающее через себя требование.

Время обслуживания – период времени, в течение которого обслуживается требование.

Если время обслуживания велико, появляется очередь, т.е. множество требований, желающих быть обслуженными, но еще не обслуженных.

Цех вместе с очередью называется системой массового обслуживания (СМО).

Работу системы массового обслуживания можно абстрактно представить следующим образом: генератор (источник) генерирует очередное требование, которое поступает в систему и либо становится в очередь на обслуживание, либо, если очереди нет, поступает в цех, где обслуживающее устройство начинает выполнять запрос на обслуживание.

Математическая модель СМО – это совокупность математических выражений, описывающих входящий поток требований, процесс обслуживания и их взаимосвязь.

Теория массового обслуживания (теория очередей) – раздел теории вероятностей, целью исследований которого является рациональный выбор структуры системы обслуживания и процесса обслуживания на основе изучения потоков требований на обслуживание, поступающих в систему и выходящие из неё, длительности ожидания и длины очередей. В теории массового обслуживания используются методы теории вероятностей и математической статистики.

Дата добавления: 2015-01-19; просмотров: 387; Нарушение авторских прав

Мы поможем в написании ваших работ!