ЦЕЛЬ И МЕТОДИКА ПОСТАНОВКИ ЛАБОРАТОРНОЙ РАБОТЫ

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Саратовский Государственный Технический Университет

Лабораторная работа по ТОЭ

«экспериментальное определение коэф­фициентов электростатической индукции, частичных емкостей и по­тенциальных коэффициентов трехжильного кабеля»

САРАТОВ 2006

ЦЕЛЬ И МЕТОДИКА ПОСТАНОВКИ ЛАБОРАТОРНОЙ РАБОТЫ

Цель работы - экспериментальное определение коэф­фициентов электростатической индукции, частичных емкостей и по­тенциальных коэффициентов трехжильного кабеля, а также проверка существующих связей между ними.

Электрическое поле системы заряженных тел имеет сложный ха­рактер и может быть рассчитано с помощью трех групп коэффициен­тов Максвелла. Эти группы формул Максвелла справедливы для си­стемы заряженных тел любой формы. Коэффициенты Максвелла исполь­зуют при расчетах не только электростатических полей, но и при расчетах быстропротекающих процессов в электрических цепях, электронных лампах и транзисторах, при емкостном отборе мощнос­ти от высоковольтной линии электропередачи и т.д.

Для примера рассмотрим трех проводку с линией (рис. I).

В системе нескольких заряжен­ных м заряд каждого тела опре­деляется не только собственным потенциалом, но также потенци­алами всех остальных тел. Указан­ное равносильно представлению, что в системе трех проводов (рис. 1.) каждый провод как бы соединен с обкладками трех конденсаторов.

Тогда заряды проводов на единицу длины можно выразить как

(1)

Система уравнений (I) есть третья группа формул Максвелла. Коэффициента С_km называется частичными емкостями, собственны­ми при одинаковых индексах и взаимными - при различных.

Систему уравнений (I) можно записать в другой форме:

где

Если обозначить = , = , = ,

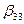то получим

(2)

Коэффициенты β_km называет емкостными, собственными при одинаковых индексах (k=m) и взаимными при k≠m. Это вторая группа формул Максвелла. Размерность емкостных коэффициентов та же, что и частичных емкостей.

Поскольку определитель системы уравнений (2) симметричен относительно главной диагонали, то ∆_km= ∆mk поэтому

Все β с одинаковыми индексами положительны, все β с различ­ными индексами отрицательны.

Систему уравнений (2) можно решить относительно потенциалов, полагая, что коэффициенты β известны

или (3)

где

(4)

Систему уравнений (3) принято называть первой группы формул максвелла. Коэффициенты α_km называет потенциальными коэффици­ентами, размерность их равна размерности единицы длины, разде­ленной на фараду. Все коэффициенты α_km положительны. При k=m - коэффициенты α_kk - называются собственными, а при k≠m - взаимными.

Потенциальные коэффициенты можно найти и непосредственно, используя метод зеркальных изображений (рис. 2). На основании анализа электростатического поля системы заряженных тел, распо­ложенных вблизи проводящей плоскости можно записать

(5)

где радиусы первого, второго и третьего проводов

соответственно(в нашем случаи );

расстояние первого провода до зеркального изобр

ажения второго провода;

расстояние первого провода до второго и т.д.

;

Коэффициенты при затратах, как видно из системы уравнений (5) зависят только с геометрических размеров тел, взаимного их расположения и от свойств среды. Они не зависят ни от величины, ни от знаков зарядов и потенциалов. Так как и

Полученные результаты можно обобщить на любую систему заря­женных проводников:

где во всех формулах

Дата добавления: 2015-06-30; просмотров: 213; Нарушение авторских прав

Мы поможем в написании ваших работ!