Нормальное или гауссовское распределение

Одним из часто встречающихся на практике распределений является нормальный или гауссовский закон. Ему подчиняются физические величины, случайность которых обусловлена действием множества независимых (или слабо зависимых) малых аддитивных факторов, результат воздействия каждого из которых мал по сравнению с их суммарным воздействием. Плотность распределения вероятности нормального закона имеет вид

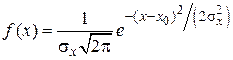, (2.9)

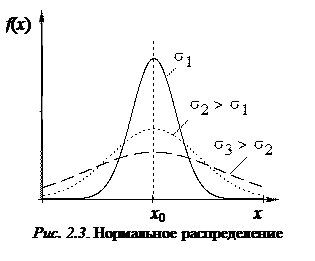
где x – случайное значение величины X. Параметр x₀ определяет центр распределения, а s_x – форму и ширину кривой плотности рас­пределения (рис. 2.3). Множитель 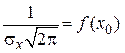перед экспонентой, определяющий высоту гауссовской кривой, выбран таким образом, чтобы было выполнено условие нормировки (2.4).

Поскольку Гауссово распределение симметрично относительно x₀, согласно (2.8) вероятность того, что случайное значение x величины X, распределенной по нормальному закону, попадет в заданный интервал (x₁, x₂), будет определяться выражением

. (2.10)

Вводя обозначение 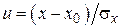, называемую стандартизованной переменной, (2.10) можно записать в виде

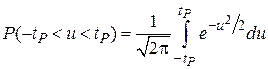, (2.11)

где t_P – коэффициенты, определяющие ширину интервала в единицах параметра нормального распределения s_x: 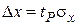. Вероятности P попадания u в интервал (–t_P, t_P) можно найти, вычислив интеграл (2.11) численно для различных значений ширины интервала t_P. И обратно, каждой заранее заданной вероятности P будет соответствовать свое конкретное значение коэффициента t_P, зависящее от выбора доверительной вероятности P. Если значения коэффициентов t_P найдены, то от переменной u можно вернуться к переменной x. Тогда из неравенства 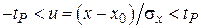получим 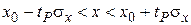с вероятностью P.

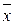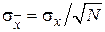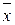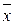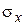Можно показать (см. 2.6), что если значения x величины X распределены по нормальному закону, то и рассчитываемые по ним средние значения также распределены по нормальному закону с центром в точке x₀ и шириной распределения , где N – объем выборок, по которым рассчитываются . Распределение средних будет описываться формулой (2.9), в которой x заменено на , а на .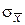

Если средние значения 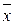распределены по нормальному закону, то задача нахождения доверительного интервала сводится к нахождению доверительного интервала (–t_P, t_P) для стандартизованной переменной 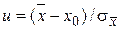и переходу к доверительному интервалу переменной 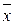. В результате получим, что границы интервала, в который случайное значение 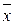попадает с вероятностью P, определяются неравенством 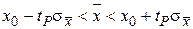. Откуда для границ доверительного интервала x₀ получаем 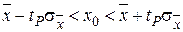, где t_P – коэффициенты, соответствующие заданной вероятности Р. Это неравенство принято записывать в виде символического равенства

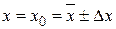с вероятностью P, (2.12)

где 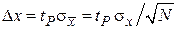– случайная доверительная погрешность результата измерения.

2.6. Выборочные дисперсия и среднеквадратичное
отклонение

В реальном эксперименте имеет место выборка конечного объема, а не генеральная совокупность, подчиняющаяся нормальному закону. Поэтому чтобы воспользоваться формулой (2.12) для определения случайной доверительной погрешности результата измерения, необходимо найти оценку параметра 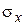и новые коэффициенты t_{P, N} (которые в этом случае будут зависеть от количества измерений N), соответствующие выборке конечного объема.

Таким наилучшим приближением, или оценкой стандартного отклонения 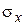, согласно (2.3) является величина

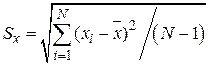, (2.13)

называемая выборочным среднеквадратичным отклонением (СКО x) результата наблюдения от среднего. Квадрат СКО 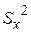называют выборочной дисперсией результата наблюдения.

Для нахождения оценки параметра 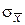рассмотрим случайную величину Z, представляющую собой сумму случайных величин X и У. Тогда среднее значение Z имеет вид

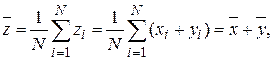
а выборочная дисперсия

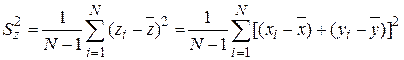
может быть представлена в виде

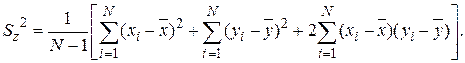
Если X и Y независимы друг от друга, то их отклонения от средних значени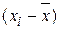й и 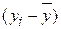также независимы. Учитывая, что среднее значение произведения независимых случайных величин равно произведению средних значений сомножителей, получим, что последняя сумма равна нулю, и S_z² = S_x² + S_y², т. е. дисперсии независимых случайных величин складываются линейно, а выборочные среднеквадратичные отклонения складываются квадратично.

Если Z = аХ + bY, то, повторив рассуждения, получим

S_z² = aS_x² + bS_y².

В случае суммы более двух случайных величин

Z = a₁X₁+a₂X₂ +…+a_NX_N = ,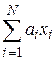

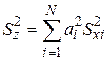. (2.14)

Для нахождения погрешности результата измерения представляет интерес не СКО результата отдельного наблюдения 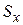, а СКО сред­него значения 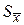. Взаимосвязь между параметрам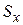и и 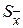можно найти, если учесть, что среднее значение есть сумма N незави­симых случайных величин, дисперсии которых одинаковы

.

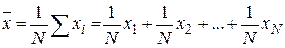Тогда, ис­пользуя формулу (2.14), в которой а_i = 1/N, с учетом 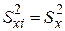получим для дисперсии параметра :

.

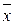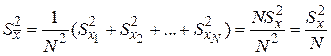Отсюда следует, что СКО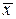

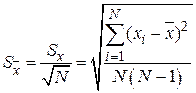. (2.15)

Параметр 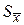, называемый выборочным среднеквадратичным отклонением среднего (СКО 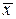), является наилучшим приближением к параметру .

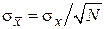Если СКО 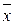найдено согласно (2.15), то, как было впервые предсказано английским математиком В. С. Госсетом, писавшим свои работы под псевдонимом Стьюдент, и впоследствии доказано Р. А. Фишером, новая стандартизованная переменная имеет функцию плотности распределения вероятности , зависящую от объема выборки N. Вероятность того, что величина u попадет в заданный интервал ( 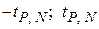), будет

,

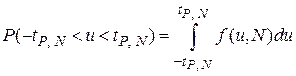откуда случайную доверительную погрешность результата измерения необходимо рассчитывать по формуле

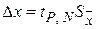, с вероятностью P,

где 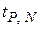– коэффициенты Стьюдента, зависящие от доверительной вероятности P и объема выборки N, по которой рассчитываются 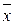и 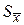. При больших значениях 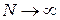(на практике при N ≥ 20) параметры 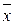и 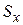, рассчитываемые по выборке конечного объема, переходят в параметры 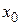и 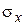нормального распределения, а коэффициенты Стьюдента t_{P, N} – в коэффициенты t_P для нормального закона.

Для проверочной оценки случайной доверительной погрешности ре­зультата измерения её расчет можно также производить по формуле Dx = b_{P, N} R, где R = x_max – x_min – размах выборки.

Значения коэффициентов t_{P, N} и b_{P, N} для данных значений дове­рительной вероятности (по договоренности в технике берут значение Р = 95 %) и числа N наблюдений в выборке приведены в приложении. В математических справочниках, как правило, коэффициенты Стьюдента приводят в таблицах в виде 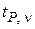, где ν = N – 1 называется числом степеней свободы выборки объема N.

Необходимо отметить, что при расчетах доверительной погреш­ности по Стьюденту результаты наблюдений должны принадлежать генеральной совокупности, распределенной по нормальному закону, что может быть проверено с помощью специальных статистических критериев. Для выполнимости этой процедуры выборка должна быть достаточно представительной (от 50 наблюдений и больше). Выборки малых объёмов (N << 15), которые имеют место в работах лабо­раторного физического практикума, на принадлеж­ность нормальному распределению не проверяют.

Дата добавления: 2015-06-30; просмотров: 496; Нарушение авторских прав

Мы поможем в написании ваших работ!