
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
III. Изучение нового материала. 1. Показательное неравенство – это неравенство, содержащее неизвестное в показателе степени
1. Показательное неравенство – это неравенство, содержащее неизвестное в показателе степени.
2. Решение неравенств.
а) Решение показательных неравенств часто сводится к решению неравенства
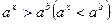 .
.
Если a>1, то функция 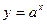 возрастает, и x>b
возрастает, и x>b 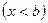 .
.
Если 0<a<1, то функция 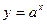 убывает, и
убывает, и 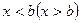 .
.
б) Некоторые показательные неравенства заменой 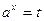 сводятся к квадратным неравенствам, которые решают, учитывая, что t>0.
сводятся к квадратным неравенствам, которые решают, учитывая, что t>0.
в) Графическое решение неравенства сводится к построению графиков функций из левой и правой частей неравенства. На интервале I большие (меньшие) значения принимает та функция, график которой расположен выше (ниже) графика другой функции.
3. №228(1, 2, 3,5) – на доске по очереди.
Запись решения:
1) 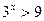
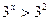 .
.
Так как функция 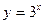 возрастает, то x>2.
возрастает, то x>2.
Ответ: 1)x>2, 2)x<2, 3)x>- 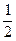 , 5)x
, 5)x 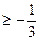 .
.
№229(1, 3) – за доской.
Ответ: 1) 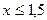 ; 3)
; 3) 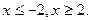
№232 – работа в группах.
Ответ: 1)x<1, 2)x>1, 3) 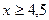 , 4)
, 4) 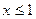 .
.
№233(1) – учитель с классом.
№233(3) – на доске по желанию.
№233(2, 4) – самостоятельно по вариантам.
Ответ: 1)х>1;2;3; х<2;-3;-2;-1;0;1; 3)х>-1;0;1;2;3; 4)х<-1;-3;-2.
№239(1) – учитель показывает на доске решение:
0,4 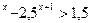
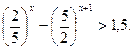
Пусть 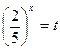 , где t>0, тогда
, где t>0, тогда
t- 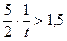
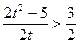
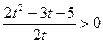
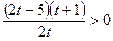
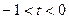 и
и 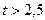 .
.
Учитывая, что t>0,
имеем: t>2,5
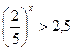
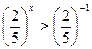
Так как функция 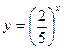 убывает, то x<-1.
убывает, то x<-1.
Ответ: x<-1.
№239(2, 3, 4) – работа в группах.
Ответ: 2)-2<x<1, 3)x>1, 4)- 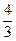 <x<2.
<x<2.
IV. Домашнее задание: №228(4, 6); №229(2, 4); №253(2, 4). Тренажер №4.
V. Итог урока. Объясните алгоритм решения показательного неравенства. На что нужно обращать особое внимание?
VI. Дополнительное задание.
№253(1, 2) – самостоятельно.
Ответ: 1) x>4, 3)x<-3 и x>1.
№261 – индивидуально по желанию.
Решение:
1)8,4 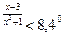 . Так как функция
. Так как функция 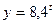 возрастает, то
возрастает, то 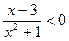 . Выражение
. Выражение 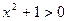 для любого действительного х, значит,
для любого действительного х, значит, 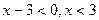 .
.
Ответ 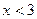 .
.
2) 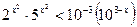
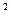
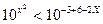
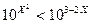
Так как функция 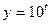 возрастает, то
возрастает, то 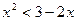
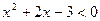 ;
; 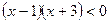
Ответ: 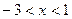 .
.
3) 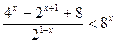
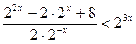 ; так как
; так как 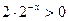 для любого х, то
для любого х, то
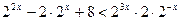
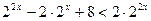
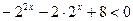 . Пусть
. Пусть 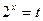 , где t>0, тогда
, где t>0, тогда
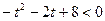 ;
;  ;
; 
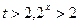 .
.
Так как функция 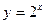 возрастает, то x>1.
возрастает, то x>1.
Ответ: x>1.
4) 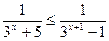 ; так как
; так как 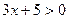 , то и
, то и 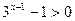 .
.
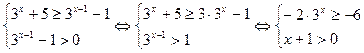
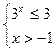 , так как функция
, так как функция 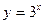 возрастает, то
возрастает, то 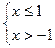
Ответ: -1<x 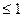 .
.
| <== предыдущая страница | | | следующая страница ==> |
| I. Организационный момент | | | II. Повторение и закрепление знаний |
Дата добавления: 2015-06-30; просмотров: 225; Нарушение авторских прав

Мы поможем в написании ваших работ!