Скорость звука в газах

Звук, распространяясь в жидкости или газе, создает области сгущения или разрежения. В областях сгущения давление повышается на по отношению к давлению газа в невозмущенной среде. В областях разрежения давление соответственно понижается. Величину избыточного давления называют звуковым давлением.

Наша цель – определить скорость волны в газе. Для нахождения скорости необходимо составить волновое уравнение . Константа, стоящая в волновом уравнении перед второй производной по координате, - это квадрат скорости волны.

Пусть в направлении ОХ в воздухе распространяется волна. Выделим цилиндрический участок среды длиной , расположенный параллельно оси.

- смещение от положения равновесия точек, находящихся в левом сечении рассматриваемого участка среды и имеющих координату х. Давление в этом сечении равно .

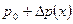- смещение от положения равновесия точек, находящихся в правом сечении рассматриваемого участка среды и имеющих координату . Давление в этом сечении равно .

Запишем для выделенного участка среды второй закон Ньютона:

В общем случае давление газа зависит от плотности и температуры . В процессе распространения волны плотность газа меняется –чередуются области сгущения и разрежения. Изменяется ли температура?

Теплопроводность газов очень плохая, это позволяет предположить, что в процессе сжатия или разрежения участка среды теплообмен с соседними участками отсутствует. Поэтому процесс распространения возмущения в газе можно считать адиабатным. Запишем уравнение Пуассона и уравнение состояния идеального газа:

где и - давление и температура в невозмущенной среде,

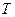и - давление и температура в какой-либо точке возмущенной среды,

- показатель адиабаты.

Преобразуя уравнения, входящие в систему, нетрудно получить соотношения: и 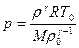. Видим, что давление является функцией одной переменной – плотности 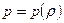. При небольших изменениях плотности отклонение давления в газе от нормального можно рассчитать следующим образом:

Производную находим в точке и 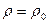. Тогда .

Изменение плотности 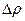находится из условия неизменности массы рассматриваемого участка среды:

где - относительное удлинение участка среды. Знак «-» указывает на то, что увеличение плотности приводит к сжатию участка среды. Подставляем полученный результат в уравнение (*) и считая :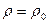

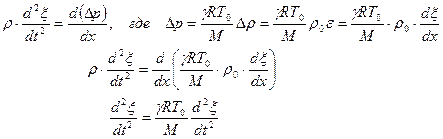
Скорость звука в газе, как это видно из волнового уравнения, равна

.

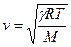При нормальных условиях в воздухе ( 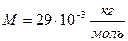и как для двухатомного газа) скорость звука равна 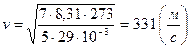. Этот результат прекрасно согласуется с опытными данными. Это подтверждает правильность предположения, что процесс распространения возмущения в газе является адиабатным.

Нетрудно видеть, что по порядку величины скорость звука в газе совпадает со средней квадратичной скоростью молекул газа . Этот факт имеет простое физическое объяснение: передача возмущения в газах осуществляется за счет теплового движения молекул!

Дата добавления: 2015-06-30; просмотров: 319; Нарушение авторских прав

Мы поможем в написании ваших работ!