ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ И ЕГО СТРУКТУРА

I О

А → I , I → I, Е → Е

Различают простое (чистое) обращение и обращение с ограничением. Простым, или чистым называется обращение без изменения количества суждения, так обращаются суждения, оба термина которых распределены или оба не распределены. Если же предикат исходного суждения не распределен, то он не будет распределен и в заключении, где он становится субъектом, т. е. его объем ограничивается. Такое обращение называется обращением с ограничением. Общеутвердительное суждение (А) обращается в частноутвердительное (I), т. е. с ограничением. Например:" Все охотники нашего общества (S +) сдали членские взносы (P -). Следовательно, некоторые сдавшие членские взносы (P -) - охотники нашего общества (S -) ". В исходном суждении предикат не распределен, поэтому он, становясь субъектом заключения, также не может быть распределен. Его объем ограничивается (" некоторые сдавшие членские взносы "). Схема обращения суждения А: Все S есть P. Некоторые P есть S распределен Общеутвердительные выделяющие суждения (в которых предикат) обращаются без ограничения по схеме: Все S, и только S, есть P. Все P есть S. Общеотрицательное суждение (Е) обращается в общеотрицательное (Е), т. е. без ограничения. Например:" Ни один следователь нашего отдела (S +) не является не юристом (P +). Следовательно, ни один не юрист (P +) не является следователем нашего отдела (S +) ". Простое обращение этого суждения возможно потому, что его предикат (" не юрист ") распределен. Схема обращения суждения Е: Ни одно S не есть P. Ни одно P не есть S

Частноутвердительное суждение (I) обращается в частноутвердительное (I). Это простое (чистое) обращение. Предикат, не распределенный в исходном суждении, не распределен в заключении. Количество суждения не изменяется. Например:" Некоторые следователи нашего отдела (S -) - юристы (P -). Следовательно, некоторые юристы (P -) - следователи нашего отдела (S -). "Схема обращения суждения I: Некоторые S есть P Некоторые P есть S Частноутвердительное выделяющее суждение (предикат распределен) обращается в общеутвердительное. Например: " Некоторые юристы (S -) являются судьями (P +). Следовательно, все судьи (P +) являются юристами (S -) ". Эти суждения обращаются по схеме: Некоторые S, и только S, есть P. Все P есть S. Частноотрицательное суждение (О) не обращается. Таким образом, обращение суждения не ведет к изменению его качества, количество может изменяться (обращение с ограничением), но может оставаться тем же самым (простое, или чистое, обращение). Умозаключения посредством обращения играют важную роль в процессе рассуждения. Благодаря тому, что предметом нашей мысли становится предмет, отраженный предикатом исходного суждения, мы уточняем наши знания, придаем им большую определенность. Необходимо, однако, строго соблюдать правила ограничения, нарушение которых ведет к ошибкам рассуждения.

3/Противопоставление предикату - это преобразование суждения, в результате, которого субъектом становится понятие, противоречащее предикату, а предикатом субъект исходного суждения. Противопоставление предикату может рассматриваться как результат превращения и обращения: превращая исходное суждение S - P, устанавливаем отношение S к не - Р; суждение, полученное путем превращения, обращается, в результате устанавливается отношение не - Р к S. Заключение, полученное посредством противопоставления предикату, зависит от количества и качества исходного суждения.

Частноутвердительные суждения (I) посредством противопоставления предикату не преобразуются.

A E

I О

А → Е , Е → I , О → I

Общеутвердительное суждение (А) преобразуется в общеотрицательное (Е).

Например: " Все адвокаты имеют юридическое образование. Следовательно, ни один не имеющий юридического образования не является адвокатом ". Схема противопоставления предикату суждения А: Все S есть P. Ни одно не - P не есть S. Правильность полученного заключения можно проверить путем последовательного применения двух логических операций: превращения и обращения. Общеотрицательное суждение (Е) преобразуется в частноутвердительное (I). Например: " Ни одно подразделение нашего РОВД не имеет плохих показателей. Следовательно, некоторые подразделения не имеющие плохих показателей являются подразделениями нашего РОВД ".

Схема противопоставления предикату суждения Е: Ни одно S не есть P. Некоторые не - P есть S. Частноутвердительное суждение (I) посредством противопоставления предикату не преобразуется. Превращение суждения : " Некоторые S есть Р " дает частноотрицательное суждение" Некоторые S не есть не - Р ". Но частноотрицательное суждение не обращается. Частноотрицательное суждение (О) преобразуется в частноутвердительное (I).

Например: « Некоторые потерпевшие не являются совершеннолетними. Следовательно, некоторые несовершеннолетние являются потерпевшими». Схема противопоставления предикату суждения О: «Некоторые S не есть Р. Некоторые не - Р есть S». Значение умозаключений посредством противопоставления предикату состоит в том, что в них выясняется отношение предметов, не входящих в объем предиката, к предметам, отраженным субъектом исходного суждения. Устанавливая отношение между этими предметами, мы уточняем наши знания, высказываем нечто новое, что не было в явной форме выражено в исходном суждении.

4)Умозаключение по логическому квадрату.

Учитывая свойства отношений между категорическими суждениями А, Е, I, О, которые иллюстрированы схемой логического квадрата, можно строить выводы, устанавливая следствие истинности или ложности одного суждения из истинности или ложности другого суждения.

А – Е - противоположность (контрарность). Из истинности одного суждения следует ложность другого суждения, но из ложности одного из них не следует истинность другого. Выводы строятся по схемам: А→ ¬ Е, Е → ¬ А, ¬ А→ ( Е v ¬ Е), ¬ Е→ ( А v ¬ А).

А – I, Е – О – подчинение. Из истинности подчиняющего суждения следует истинность подчиненного суждения, но не наоборот: из истинности подчиненного суждения истинность подчиняющего суждения не следует, оно может быть истинным, но может быть ложным. Выводы строятся по схемам: А → I, Е → О, I → (А v ¬А), О → (Е v ¬ Е), ¬I →¬А, ¬ О →¬ Е,

¬ А → (I v ¬ I), ¬ Е →(О v ¬ O).

I - О - частичная совместимость (субконтрарность). Истинными могут быть оба суждения, но не могут быть вместе ложными, по крайней мере, одно из них истинно. Из ложности одного суждения следует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность другого суждения.

Выводы строятся по схемам: ¬I → О, ¬ О → I, I → (О v ¬ О), О → (I v ¬ I).

А – О, Е - I - противоречие (контрадикторность). Из истинности одного суждения следует ложность другого суждения, из ложности одного – истинность другого. Выводы строятся по схемам: А →¬ О, ¬ А→ О, Е →¬ I, ¬ Е→ I.

Непосредственные умозаключениявозможны здесь потому, что между суждениями, находящимися в этих отношениях, существуют определенные зависимости по истинности и ложности. Учитывая, что каждое суждение - А, Е, I, О - может находиться в трех отношениях с другими, из него можно сделать 3 вывода. Пример, если истинно общеутвердительное суждение (А), что «Все благородные мысли находят в себе сочувствие», то отсюда следует:

1) что тем более истинно частноутвердительное суждение (I): «Некоторые благородные мысли находят себе сочувствие» (отношение подчинения); 2) что ложно общеотрицательное суждение (Е): «Ни одна благородная мысль не находит себе сочувствия» (отрицание противоположности); 3) что ложно частноотрицательное суждение (О): «Некоторые благородные мысли не находят себе сочувствия» (отношение противоречия). Другой пример, если ложно общеутвердительное суждение (А), что «Все юристы имеют специальное высшее образование» (так как есть еще среднее юридическое), то отсюда можно сделать выводы: 1) что истинно частноотрицательное суждение (О): «Некоторые юристы не имеют высшего образования» (отношение противоречия); 2) что в данном случае ложно общеотрицательное суждение (Е): «Ни один юрист не имеет высшего образования» (отношение противоположности); 3) что в данном случае истинно частноутвердительное суждение (I): «Некоторые юристы имеют высшее образование» (отношение подчинения).

Из приведенных примеров следует, что знание зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рассуждения. Умозаключения «по логическому квадрату» находят применение во многих мыслительных приемах и операциях, в том числе и в аргументации, где построение некоторых способов косвенного доказательства и косвенного опровержения опираются на отношение противоречия. Аристотель разработал теорию и правила дедуктивных умозаключений – движения мысли от общего к частному.

Аристотель: “Мы полагаем, что знаем каждую вещь безусловно, А НЕ СОФИСТИЧЕСКИ, ПРИВХОДЯЩИМ ОБРАЗОМ, когда полагаем, что знаем причину, в силу которой она есть, что она действительно причина ее и что иначе обстоять не может”

(Аристотель. О софистических опровержениях // Соч. в 4-х томах, т.2, с.259)

Софисты постоянно нарушают законы и правила правильного мышления при использовании понятий и суждений, то есть при построении дедуктивных умозаключений (общих посылок и выводов из посылок).

Они рассуждают так:

1. Сократ – человек.

2. Кориск – не Сократ.

3. Следовательно, Кориск – не человек.

Аристотель понял, что опровергнуть эти умозаключения можно лишь зная правила построения умозаключений. Все работы по логике у Аристотеля написаны в плане разработки законов и правил дедуктивных умозаключений. Структуру дедуктивного умозаключения он называет силлогизмом. Везде он приводит десятки и сотни аргументов, разоблачающих неправильные силлогизмы софистов.

Аристотель открыл и утвердил в логику АКСИОМУ (положение нетребующее доказательства) СИЛЛОГИЗМА:

« Что утверждается или отрицается относительно всего класса вещей, может утверждаться или отрицаться и относительно каждой вещи, входящей в этот класс».

Простой категорический силлогизм есть вид умозаключения (более общо – форма мысли), в котором из двух исходных истинных простых категорических суждений (называемых посылками), связанных между собой определенным образом (по среднему термину), выводится новое по содержанию суждение (называемое выводом, следствием, заключением). В целом, данное умозаключение состоит из трех простых категорических суждений, два из которых — посылки, третье — вывод. Однако, выделяя в качестве элементов умозаключения лишь суждения (посылки и вывод), закономерную связь между ними уловить трудно. Эту связь значительно легче обнаружить, выделяя в категорическом умозаключении и входящие в посылки термины (понятия). Так как субъектно-предикатная запись суждений одинакова для всех видов суждений, то, чтобы отличить субъект или предикат вывода от субъектов и предикатов посылок, следует уточнить нашу символику.

В простом категорическом силлогизме символом «S», как и обычно, обозначается субъект вывода и соответствующее ему понятие в посылке. Это - меньший термин. Символом «P» обозначается предикат вывода и соответствующее понятие в посылке. Это — больший термин. А то понятие, которое является общим для обеих посылок, т.е. имеется в обоих исходных суждениях, но отсутствует в самом заключении, обозначим символом «M».
Это — средний термин категорического силлогизма. Приведем пример простого категорического силлогизма, используя эту символику:

Все студенты - учащиеся
Некоторые спортсмены - студенты
Некоторые спортсмены - учащиеся
в формульном виде будет выглядеть так:

M – P

S - M

S - P

Общим в этом примере для посылок является понятие о студентах, это – средний термин. Он занимает место субъекта в первой посылке и место предиката во второй. Субъектом вывода является понятие о некотором конкретном (этом) человеке, предикатом вывода — понятие об учащихся.

Посылка (исходное суждение), в которой находится субъект вывода (меньший термин), называется меньшей посылкой, а исходное суждение, в котором находится предикат вывода (больший термин), называется большей посылкой. Понятно, что средний термин в посылках выполняет роль связующего звена между субъектом и предикатом вывода, между этими крайними терминами умозаключения. В круговых схемах данное
умозаключение выражается следующим образом:

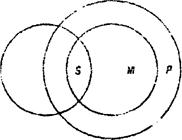
На этой схеме достаточно наглядно видно, почему субъект вывода - меньший термин, а предикат вывода - больший. Таким образом, по-другому, структуру простого категорического силлогизма составляют три и только три термина: меньший, средний и больший.

Посылками в данном силлогизме могут выступать известные нам четыре вида простых категорических суждений: общеутвердительное, общеотрицательное, частноутвердительное и частноотрицательное. Сочетания этих суждений, могущих быть посылками умозаключения, подчиняются определенным требованиям логики, выступающими законами данной структурированной организации, законами данной формы
мысли, т.е. законами простого категорического силлогизма. Эти требования формируют две группы правил для данного умозаключения: правила посылок и правила терминов.

Правила посылок:

а) из двух отрицательных посылок (т.е. из двух исходных простых
категорических отрицательных суждений) вывод с необходимостью не следует;

б) из двух частных посылок вывод тоже с необходимостью не следует;

в) если одна из посылок — суждение отрицательное, то и вывод будет необходимо отрицательным;

г) если одна из посылок — суждение частное, то и вывод будет необходимо частным.

Понятно, что если среди посылок одна частная, а другая отрицательная, или если одна из посылок — частноотрицательное суждение, то и вывод будет обязательно частноотрицательным; так же понятно, что из двух положительных посылок отрицательный вывод не следует (первые четыре правила посылок являются определяющими, остальные — производными).

Правила терминов:

а) в простом категорическом силлогизме должно быть три и только три термина: меньший, средний, больший;

б) средний термин должен быть распределен (взят в полном своем объеме, или в полном объеме должен исключаться из рассмотрения), хотя бы в одной из посылок;

в) термин, не распределенный в посылке, не может быть распределен в заключении.

Обратите внимание на основные 4 фигуры простого категорического силлогизма и их 19 правильных сочетаний (модусов). Запомните основные правила категорических силлогизмов:

1). В силлогизме должны быть три суждения: две посылки и вывод. Обе посылки должны быть истинными или правдоподобными.

2). Нельзя учетверять термины.

3). Средний термин (“М”) хотя бы раз должен браться во всем объеме, то есть быть распределенным на весь класс вещей, предметов мысли. Иначе вывод будет ошибочным.

4). Термины “S” и “Р” , взятые в посылках не во всем объеме, не могут быть в выводе выраженными во всем объеме.

5). Из двух отрицательных посылок нельзя делать никакого вывода.

6). При одной отрицательной посылке выводы могут быть только отрицательные. В частности, по 2-ой фигуре выводы могут быть только отрицательные, потому что, когда обе посылки положительные, то средний термин “М” оказывается не распределенным (нарушается 3-е правило).

Правила 7 и 8 о частных посылках.

7). Нельзя делать выводы из двух частных посылок. Тут нет определенности.

8). Восьмое правило требует частных выводов при наличии одной частной посылки.

Дата добавления: 2014-02-26; просмотров: 746; Нарушение авторских прав

Мы поможем в написании ваших работ!