
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Решение. Предположим, что многочлен 3x2n + Axn + 2 делится на многочлен 2x2m + Axm + 3
Предположим, что многочлен 3x2n + Axn + 2 делится на многочлен 2x2m + Axm + 3. Тогда любой корень многочлена 2x2m + Axm + 3 является также корнем многочлена 3x2n + Axn + 2. Если xi — корень многочлена 2x2m + Axm + 3, то xim = 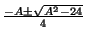 = α1,2. Можно считать, что x1m = α1 и x2m = α2. Пусть β1,2 =
= α1,2. Можно считать, что x1m = α1 и x2m = α2. Пусть β1,2 = 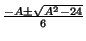 — корни квадратного трёхчлена 3x2 + Ax + 2.
— корни квадратного трёхчлена 3x2 + Ax + 2.
Первый случай. A2 - 24 > 0. В этом случае |α1| ≠ |α2|, поэтому x1n = β1 и x2n = β2. С одной стороны, |x1x2| = 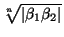 =
= 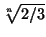 < 1, а с другой стороны |x1x2| =
< 1, а с другой стороны |x1x2| = 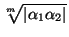 =
= 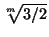 > 1. Приходим к противоречию.
> 1. Приходим к противоречию.
Второй случай. A2 - 24 ≤ 0. В этом случае |α1| = |α2| = 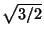 и |β1| = |β2| =
и |β1| = |β2| = 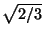 . Поэтому, с одной стороны, |x1| =
. Поэтому, с одной стороны, |x1| = 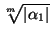 =
= 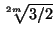 > 1, а с другой стороны, |x1| =
> 1, а с другой стороны, |x1| = 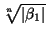 =
= 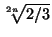 < 1. Снова приходим к противоречию
< 1. Снова приходим к противоречию
24. Докажите, что при нечетном n > 1 справедливо равенство
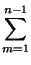
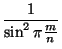 =
= 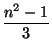 .
.
| <== предыдущая страница | | | следующая страница ==> |
| | | Введение. Электродинамика является одним из фундаментальных разделов современной классической физики |
Дата добавления: 2015-06-30; просмотров: 201; Нарушение авторских прав

Мы поможем в написании ваших работ!