
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Шесть способов доказательства теоремы Пифагора
4.1. Древнекитайское доказательство[4]
На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной a+b, а внутренний – квадрат со стороной с, построенный на гипотенузе
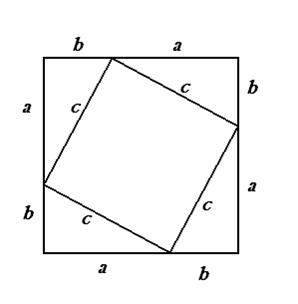
a2 + 2ab +b2 = c2 + 2ab
a2 +b2 = c2
4.2. Доказательство Дж. Гардфилда (1882 г.)[4]
Расположим два равных прямоугольных треугольника так, чтобы катет одного из них был продолжением другого.
Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту 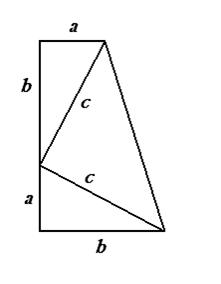
S =
C другой стороны, площадь трапеции равна сумме площадей полученных треугольников:
S =
Приравнивая данные выражения, получаем:
или с2 = a2 + b2
| <== предыдущая страница | | | следующая страница ==> |
| Из истории теоремы Пифагора | | | Старейшее доказательство |
Дата добавления: 2015-06-30; просмотров: 370; Нарушение авторских прав

Мы поможем в написании ваших работ!