Теорема умножения вероятностей зависимых событий

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого: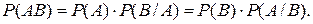

Задачи для самостоятельного решения.

№1. Студент пришёл на зачёт, зная из 30 вопросов только 24. Преподаватель задаёт 3 вопроса. Зачёт будет сдан, если студент ответит хотя бы на два вопроса из трёх. Какова вероятность того, что студент сдаст зачёт?

№2. Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) один элемент выйдет из строя; в) хотя бы один элемент выйдет из строя.

№3. Слово «вероятность» составлено из карточек разрезной азбуки. Все карточки перемешивают, затем наугад достают 4 и выкладывают в ряд. Какова вероятность получить слово «рост»?

№4. На стеллаже библиотеки в случайном порядке расставлены 15 учебников, причём 5 из них в переплёте. Библиотекарь берёт наудачу 4 учебника. Найти вероятность того, что, по крайней мере, два из них в переплёте.

----------------------------------------------------------------------------------------------------------------

Теоремы сложения и умножения вероятностей. Стр.1

№5. Вероятность попадания в мишень для первого спортсмена 0,85, а для второго – 0,8. Спортсмены независимо друг от друга делают по одному выстрелу. Найти вероятность того, что в мишень попадёт хотя бы один спортсмен.

№6. В урне 6 голубых, 5 красных и 4 белых шара. Из урны поочерёдно извлекают шар, не возвращая его обратно. Найти вероятность, что при первом извлечении появится голубой шар, при втором – красный, при третьем – белый.

№7. Имеются две урны с шарами трёх цветов. В первой находятся 2 голубых, 3 красных, 5 зелёных, а во второй – 4 голубых, 2 красных, 4 зелёных. Из каждой урны извлекают по одному шару и сравнивают их цвета. Найти вероятность того, что цвета вынутых шаров одинаковы.

№8. Рабочий обслуживает четыре однотипных станка. Вероятность того, что любой станок в течение часа потребует внимания рабочего равна 0,6. Предполагая, что неполадки на станках независимы, найти вероятность того, что в течение часа потребуют внимания рабочего: а) все четыре станка; б) один станок; в) по крайней мере один станок.

№9. Слово «папаха» составлено из букв разрезной азбуки. Все карточки тщательно перемешаны. Четыре карточки извлекаются по очереди и раскладываются в ряд. Какова вероятность получить таким путём слово «папа»?

№10. Известно, что курс евро к рублю может возрасти с вероятностью 0,55, а курс доллара к рублю может возрасти с вероятностью 0,35. Вероятность того, что возрастут оба курса, составляет 0,3. Найти вероятность того, что курс евро или доллара по отношению к рублю возрастёт.

№11. Талантливый сантехник Гриша обязательно раз в неделю напивается «до чёртиков» (только раз, но обязательно). Найти вероятности следующих событий: а) Гриша напьётся во вторник, если он был трезв в понедельник; б) Гриша будет трезв в среду и четверг, если он не пил в понедельник и во вторник; в) Гриша будет пьян в один день с электриком Колей, который ведёт себя так же, но независимо от Гриши.

№12. Сколько раз нужно бросить игральную кость, чтобы вероятность выпадения хотя бы один раз грани «6» была больше 0,9?

№13. Два игрока поочерёдно бросают монету. Выигрывает тот, у которого первым выпадет «герб». Какова вероятность выигрыша для игрока, бросающего монету первым?

Дата добавления: 2015-06-30; просмотров: 396; Нарушение авторских прав

Мы поможем в написании ваших работ!