
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Расход воды на одного человека в России и сопутствующие ему потери
| Год | Расход воды на одного человека, л/сут | Потери, % | |
| Всего | В том числе горячей | ||
Таким образом, приведенные соображения объективно подтверждают необходимость перехода от систем дроссельного регулирования насосных агрегатов к системам автоматического управления ими путем автоматического поддержания необходимого технологического параметра, в частности, напора (давления) при изменяющемся расходе воды за счет применения частотно-регулируемых асинхронных электроприводов [5, 7, 8, 9].
Возможности энергосберегающего управления при регулировании скорости электропривода по сравнению с дроссельным регулированием проиллюстрированы на рис. 2.5. За счет уменьшения скорости насос работает при снижении расхода в точке С на кривой 2 при неизменной характеристике магистрали (кривая 3). Мощность, потребляемая электроприводом в этом случае, пропорциональна площади прямоугольника 0ECF, что наглядно иллюстрирует возможности существенного снижения энергопотребления при внедрении регулируемых электроприводов насосов. Наряду с этим уменьшается при снижении расхода воды и напор в системе, что приводит к уменьшению потерь (утечек) воды.
Приведем методики для приближенной сравнительной оценки энергопотребления при изменении подачи центробежных насосов за счет дроссельного регулирования (ДР) и частотного регулирования (ЧР) скорости АД насоса [6].
Как указывалось выше, установившийся режим работы насосной установки при постоянной скорости приводного электродвигателя определяется точкой пересечения характеристики насоса, соответствующей этой частоте, и характеристики магистрали, подключенной к насосу. Характеристикой насоса является зависимость напора Н от расхода Q, которую с достаточной степенью точности можно представить в виде:
 , (2.12)
, (2.12)
где Н0н – напор насоса при Q = 0 и ω = ωном; ωном – номинальная скорость электродвигателя; С – конструктивный коэффициент насоса, С = (Н0н-Нном)/Qном2; Qном и Нном – номинальные расход и напор.
Характеристика магистрали определяется следующим выражением:
 , (2.13)
, (2.13)
где Нс – статический напор (противодавление), соответствующий Q = 0 (закрытой задвижке); R – коэффициент сопротивления магистрали, R=(Нном-Нс)/Qном2.
Характеристики способов регулирования центробежного насоса и магистрали приведены на рис. 2.7.
Мощность, потребляемая насосной установкой из сети:
 ,
,
где Рмех – мощность на валу двигателя насоса, Рмех = Мсω; Мс – статический момент нагрузки на валу двигателя; η1 – КПД двигателя.
Регулирование подачи дроссельной заслонкой основано на изменении сопротивления магистрали. В этом случае при ω = ωном = const рабочая точка механизма перемещается по Q–Н-характеристике, соответствующей номинальной скорости двигателя, в сторону снижения подачи до точки пересечения с новой характеристикой магистрали (точки 1, 2, 3 на рис. 2.7).
При электрическом способе регулирования подачи рабочая точка перемещается по неизменной характеристике магистрали (точки 4, 5, 6, 7 на рис. 2.7). При этом с уменьшением подачи уменьшается и требуемый напор, что приводит к снижению статической мощности, необходимой для работы насоса с заданным расходом воды, по сравнению с дроссельным регулированием.
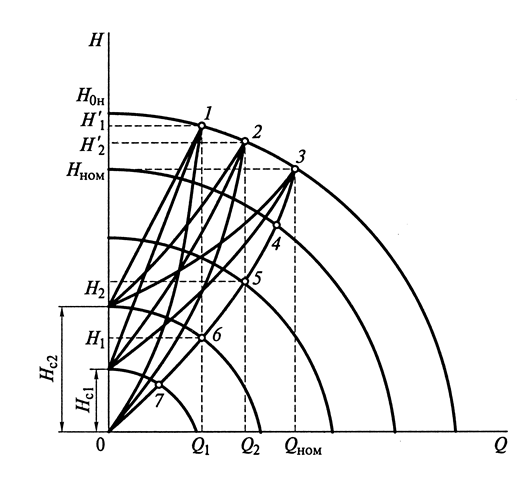
Рис. 2.7. Характеристики способов регулирования центробежного насоса:
1, 2, 3 – рабочие точки при дроссельном регулировании подачи; 4, 5, 6, 7 – рабочие точки при регулировании подачи за счет изменения частоты вращения двигателя
Рассмотрим КПД двигателя при различных способах регулирования подачи без учета потерь в стали и потерь от тока холостого хода.
При частотном управлении, осуществляемом при постоянстве абсолютного скольжения,
 ,
,
где Sном – номинальное скольжение двигателя; а – отношение активных сопротивлений фазы статора R1 и ротора R’2, a = R1/R’2.
При регулировании дроссельной заслонкой, когда ω = ωном = const, КПД двигателя постоянный и вычисляется по формуле η1 = (1-Sном)/(аSном+1).
Чтобы получить расчётные выражения в функции от расхода, скольжение двигателя можно выразить через расход. Для этого в формуле (2.12) заменим (ω/ωном)2 на [(1-S)/(1-Sном)]2 и, решив его совместно с выражением (2.13) относительно S, получим
 , (2.14)
, (2.14)
где hc = Hc/H0н; Q* = Qном;  .
.
Зависимость выраженного в относительных единицах момента на валу турбомеханизма при работе его на сеть с постоянными параметрами имеет вид
 , (2.15)
, (2.15)
где μ – относительный момент на валу турбомеханизма, μ = М/Мсmax (Мсmax – максимальный статический момент на валу механизма, который имеет место при ω= =ωном); μ0с – статический момент на валу (М0с) при Q* = 0 (закрытой задвижке), выраженный в относительных единицах, μ0с = М0с/Мсmax.
Выражения (2.14) и (2.15) позволяют выразить момент, КПД, скорость и мощность, потребляемую из сети, в функции от расхода воды при заданном противодавлении. Для универсального использования расчётных формул целесообразно определять мощность Р1 в относительных единицах (Р1* = Р1/Рб), приняв в качестве базового значения мощности Рб максимальную статическую мощность на валу двигателя Рсmax при ω = ωном, т.е. Рб = Рсmax= Мсmaxωном.
Если считать, что Мсmax = Мном (Мном – номинальный момент двигателя, Мном = =Рном/ωном), то базовая мощность Рб = Рном.
Выражения для расчёта Р1* при различных способах регулирования подачи насоса принимают следующий вид:
при дроссельном регулировании
 , (2.16)
, (2.16)
при частотном регулировании
 . (2.17)
. (2.17)
Выражения (2.16) и (2.17) позволяют рассчитать потребляемую насосом мощность при дроссельном и частотном регулировании в зависимости от расхода жидкости Q* и произвести сравнительную оценку для рассматриваемых способов регулирования. Как следует из (2.16) и (2.17), при дроссельном регулировании для заданного значения Q* потребляемая мощность Р1* зависит от μ0с, а, Sном, а при частотном регулировании – от hс, μ0с, а, Sном. Задавая эти параметры для конкретных условий работы насосного агрегата и выбранного двигателя или отрезка серии двигателей, можно рассчитать значения Р1* = f(Q*). В табл. 2.3 приведены относительные значения потребляемой мощности Р1* в функции относительного расхода Q* для дроссельного и частотного регулирования при μ0с = 0,4; а = 1; Sном = =0,04.
Используя формулы (2.16) и (2.17), можно получить известные зависимости, иллюстрирующие выигрыш в потреблении активной энергии при частотном регулировании по сравнению с дроссельным регулированием. На рис. 2.8 приведены зависимости Р1* = f(Q*) при дроссельном и частотном регулировании, построенные по данным табл. 2.3 для hс = 0. Задавая расход (Qi*) можно рассчитать потребляемую мощность при дроссельном (P1i*1) и частотном регулировании (P1i*2) и определить выигрыш в потребляемой мощности ΔP1*I = P1i*1 - P1i*2, что позволяет рассчитать снижение годовых затрат по стоимости электроэнергии при частотном регулировании асинхронных электроприводов насосных агрегатов по сравнению с дроссельным регулированием.
Как следует из табл. 2.3, с увеличением статического напора hс снижается экономия электроэнергии при внедрении частотно-регулируемого асинхронного электропривода, однако при любых значениях hс система технологической автоматизации обеспечивает поддержание постоянного давления в системе независимо от расхода, что позволяет избегать ненужных избытков давления, свойственных дроссельному регулированию. Это очень важно, так как в коммунальной сфере для существующих систем, не находящихся в аварийном состоянии, каждая лишняя атмосфера, а это давление 10 м водяного столба, вызывает дополнительно 2…7 % потерь воды за счёт утечек [6].
Таблица 2.3
| <== предыдущая страница | | | следующая страница ==> |
| Электроприводы центробежных насосов | | | Потребляемая электроприводом центробежного насоса мощность при дроссельном и частотном регулировании в зависимости от расхода жидкости и статического напора |
Дата добавления: 2015-06-30; просмотров: 150; Нарушение авторских прав

Мы поможем в написании ваших работ!