
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Дерево вероятностей
Для решения задач, в которых решения принимаются в условиях стохастической неопределенности, удобно использовать так называемое «дерево вероятностей».
Определение. Деревом вероятностей называется графический метод, который показывает последовательность стратегических решений и предполагаемые последовательности действий при каждом возможном блоке случайных обстоятельств.
Построение дерева решения начинается с первого решения и продвигается вперед через ряд последовательных событий и решений, при этом вероятностные события обозначаются кружками, а принимаемые решения квадратиками. Ответвления из квадратиков представляют стратегии, а ответвления из кружков - внешние условия. При каждом решении или событии у дерева вероятностей появляются ответвления, которые показывают соответственно возможное направление действий до тех пор, пока, наконец, все логические последовательности решений и вытекающие из них события не будут вычерчены. Отметим, что ответвления из кружков имеют вероятности, причем сумма вероятностей для всех ответвлений, вытекающих из любого кружка, должна равняться единице.
Из формулы полной вероятности следует, что для вычисления вероятности события 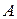 необходимо осуществить перебор всех путей, ведущих к результирующему событию
необходимо осуществить перебор всех путей, ведущих к результирующему событию 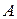 ;вычислить и расставить на соответствующих путях вероятности
;вычислить и расставить на соответствующих путях вероятности 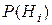 того, что движение будет происходить по данному пути, и вероятности
того, что движение будет происходить по данному пути, и вероятности 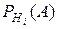 того, что на данном пути будет достигнуто конечное событие
того, что на данном пути будет достигнуто конечное событие 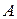 .Затем вероятности, стоящие на одном пути, перемножаются, а результаты, полученные для различных путей, складываются.
.Затем вероятности, стоящие на одном пути, перемножаются, а результаты, полученные для различных путей, складываются.
Каждое из условий может, в свою очередь, делиться на несколько дополнительных условий или гипотез, т.е. на каждом этапе оно допускает неограниченное число ветвлений схемы, поэтому при решении задач более удобно пользоваться не самой формулой полной вероятности, а графической схемой полной вероятности или соответствующим деревом вероятностей.
Пример. Трое преподавателей принимают экзамен в группе из 30 человек, причем первый опрашивает 6 студентов, второй — 3, а третий — 21 студента (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40 %, у второго — только 10 %, зато у третьего — 70 %. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен. Решение.Обозначим через 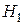 ,
, 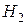
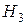 — гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи
— гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи
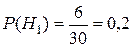
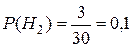
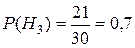
Пусть событие 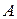 состоит в том, что слабо подготовившийся студент сдал экзамен. Тогда по условию задачи
состоит в том, что слабо подготовившийся студент сдал экзамен. Тогда по условию задачи
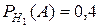
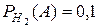
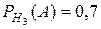 .
.
По формуле полной вероятности получаем
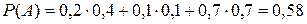 .
.
Построим для рассматриваемой задачи дерево решений


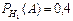

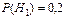
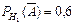





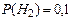
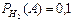
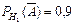


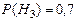
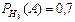
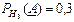
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. Пример. В трех одинаковых урнах находятся шары | | | Формула Байеса |
Дата добавления: 2015-06-30; просмотров: 427; Нарушение авторских прав

Мы поможем в написании ваших работ!