Повторные независимые испытания. Формула Бернулли

Рассмотрим схему независимых испытаний или схему Бернулли, которая имеет важное научное значение и разнообразные практические применения.

Пусть производится 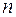независимых испытаний, в каждом из которых может произойти некоторое событие .

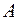Определение. Испытания называются независимыми, если в каждом из них событие 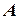наступает с одной и той же вероятностью 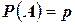, не зависящей от того появилось или не появилось событие 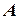в других испытаниях.

Пример. На испытательный стенд поставлены 20 ламп накаливания, которые испытываются под нагрузкой в течении 1000 часов. Вероятность того, что лампа выдержит испытание, равна 0,8 и не зависит от того, что случилось с другими лампами.

В этом примере под испытанием понимается проверка лампы на ее способность выдержать нагрузку в течении 1000 часов. Поэтому число испытаний равно . В каждом отдельном испытании возможны только два исхода:

1)событие 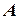, состоящее в том, что лампа выдержала испытание, произошло. Вероятность этого события 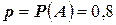и не зависит от исходов остальных испытаний.

2)событие 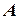не произошло, т.е. наступило событие 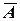, состоящее в том, что лампа не выдержала испытания. Вероятность этого события .

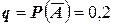Определение. Серия повторных независимых испытаний, в каждом из которых событие 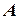наступает с одной и той же вероятностью 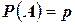, не зависящей от номере испытания, называется схемой Бернулли.

Вероятность противоположного события 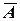обозначают 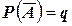, причем, как было доказано выше,

.

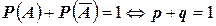Теорема. В условиях схемы Бернулли вероятность того, что при 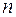независимых испытаниях событие 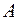появится 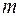раз, определяется по формуле

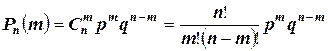, (1)

где 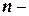число проведенных независимых испытаний;

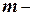число появлений события ;

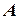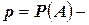вероятность наступления события 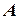в отдельном испытании;

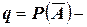вероятность не наступления события 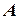в отдельном испытании;

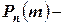вероятность того, что в 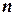независимых испытаниях события 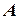произойдет

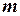раз.

Формула (1) называется формулой Бернулли или биномиальной формулой, т.к. ее правая часть является 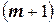членом бинома Ньютона

.

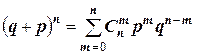Теорему примем без доказательства.

Пример. Производится 6 выстрелов по цели. Вероятность попадания в цель при каждом выстреле равна 0,7. найти вероятность того, что произойдет 2 попадания.

Запишем, прежде всего, условие задачи, вводя соответствующие обозначения.

Дано: событие 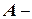попадание при отдельном выстреле;

.

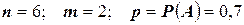Найти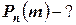

Решение.

Дата добавления: 2015-06-30; просмотров: 334; Нарушение авторских прав

Мы поможем в написании ваших работ!