Метод Гаусса

(метод последовательного исключения переменных)

На практике чаще всего применяется метод Гаусса – построения решения систем линейных уравнений.

При исследовании и решении систем линейных уравнений производятся элементарные преобразования строк расширенной матрицы 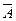, в результате которых получится ступенчатая расширенная матрица некоторой новой системы, эквивалентной данной:

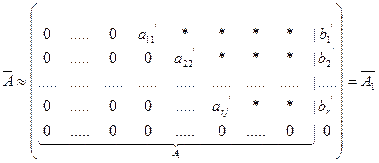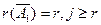, (5.1).

Выберем в матрице 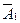ненулевой минор порядка 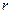, т.е. базисный минор (его можно выбрать на пересечении первых 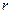строк и столбцов, с которых начинаются ненулевые элементы строк). Будем считать, что этот минор расположен в левом верхнем углу матрицы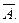

Этот минор является верхнетреугольным и равен произведению .

Нулевые строки матрицы отбросим

(им соответствуют уравнения ).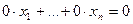

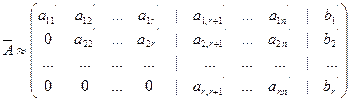(5.2)

(отбросили нулевые столбцы и перенумеровали переменные).

Все элементы базисного минора выше главной диагонали можно сделать равными нулю, а элементы главной диагонали равными единице. Таким образом, исходная система (4.1) приведена к эквивалентной системе:

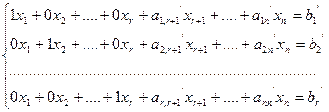(5.3),

или к системе 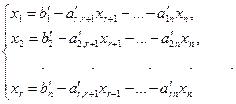(5.4)

из которой видно, что если 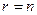, то система (5.4) имеет единственное решение:

, …, .

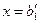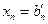Если 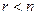, то переменные 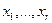– базисные, 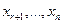– свободные и придавая им произвольные значения 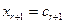, …, , 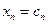можно записать общее решение системы в виде:

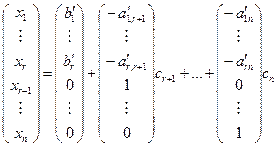(5.5).

Итак, метод Гаусса состоит в следующем:

1) расширенную матрицу системы элементарными преобразованиями приводят к ступенчатому виду;

2) сравнивают ранги основной и расширенной матриц и делают вывод о совместности или несовместности системы;

3) в случае совместности системы в основной матрице выбирают базисный минор и дальнейшими элементарными преобразованиями строк добиваются того, чтобы в этом миноре все элементы вне главной диагонали стали равными нулю, а элементы главной диагонали стали равными единице;

4) выписывают систему, соответствующую полученной расширенной матрице, после чего переписывают систему, оставляя базисные неизвестные слева и переведя остальные слагаемые в правую часть;

5) если ,то в правой части стоят только свободные члены и получено единственное решение;

6) если 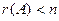, то в правой части есть свободные неизвестные. Придавая им произвольные значения, получаем общее решение по формуле (5.5).

Дата добавления: 2015-06-30; просмотров: 249; Нарушение авторских прав

Мы поможем в написании ваших работ!