
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Функции от случайных векторов
Пусть 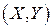 – двумерный случайный вектор с заданным законом распределения и случайная величина
– двумерный случайный вектор с заданным законом распределения и случайная величина 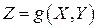 , где
, где 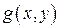 – неслучайная скалярная функция двух переменных, область определения которой содержит множество возможных значений вектора
– неслучайная скалярная функция двух переменных, область определения которой содержит множество возможных значений вектора 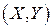 . Рассмотрим задачу нахождения закона распределения случайной величины
. Рассмотрим задачу нахождения закона распределения случайной величины 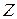 .
.
Предположим вначале, что 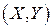 – дискретный случайный вектор, принимающий конечное число значений
– дискретный случайный вектор, принимающий конечное число значений 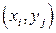 с вероятностями
с вероятностями 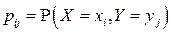 ,
, 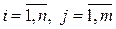 (случай счетного числа значений случайного вектора рассмотреть самостоятельно). Тогда
(случай счетного числа значений случайного вектора рассмотреть самостоятельно). Тогда 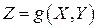 – дискретная случайная величина и ее возможными значениями
– дискретная случайная величина и ее возможными значениями 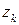 ,
, 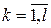 являются различные среди значений
являются различные среди значений 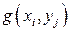 (
( 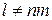 может быть). При этом вероятности значений
может быть). При этом вероятности значений 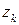 аналогично одномерному случаю определяются по формуле:
аналогично одномерному случаю определяются по формуле:
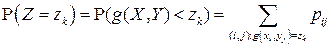 ,
, 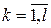 . (4.8)
. (4.8)
Если 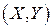 – непрерывный случайный вектор с плотностью вероятностей
– непрерывный случайный вектор с плотностью вероятностей 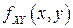 , а функция
, а функция 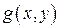 дифференцируема по каждому из своих аргументов, то
дифференцируема по каждому из своих аргументов, то 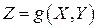 является непрерывной случайной величиной. При этом функция распределения
является непрерывной случайной величиной. При этом функция распределения 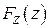 случайной величины
случайной величины 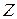 определяется формулой:
определяется формулой:
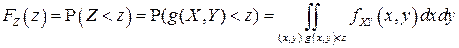 , (4.9)
, (4.9)
а плотность вероятностей 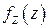 находится дифференцированием
находится дифференцированием 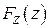 по
по 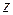 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Функции от случайных величин | | | Композиция (свертка) законов распределения |
Дата добавления: 2015-06-30; просмотров: 301; Нарушение авторских прав

Мы поможем в написании ваших работ!