Сходимость распределений (слабая сходимость)

Ранее были введены три вида сходимости последовательностей случайных величин: по вероятности, почти наверное и в среднем. Еще один вид сходимости основан на близости законов распределения случайных величин, то есть на сходимости последовательности их функций распределения.

Пусть заданы последовательность случайных величин 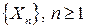, имеющих функции распределения , и случайная величина с функцией распределения 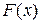. Было бы естественно считать, что, если случайная величина 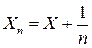, то ее закон распределения сходится при 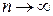к закону распределения случайной величины . Однако, требовать при этом равномерную сходимость к 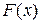(то есть, чтобы ) в общем случае неразумно, поскольку она никогда не будет иметь места, если функция распределения случайной величины имеет хотя бы один разрыв. Поэтому сходимость последовательности функций распределения к функции распределения 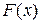понимают в смысле следующего определения.

Определение. Говорят, что последовательность функций распределения 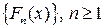слабо сходится к функции распределения 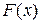и обозначают 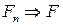, если

в каждой точке 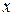, где предельная функция распределения 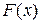является непрерывной.

При этом также говорят, что последовательность случайных величин 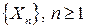слабо (или по распределению) сходится к случайной величине и записывают (или ) или, что последовательность случайных величин 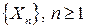слабо сходится к распределению и обозначают .

Смысл слабой сходимости: это поточечная сходимость функций распределения во всех точках непрерывности предельной функции распределения.

Выделим важный частный случай, когда предельная функция распределения 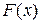является непрерывной для любого . При этом 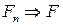, если для любого и, более того, в силу монотонности и ограниченности функций распределения сходимость является равномерной по 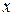: (подробнее см. учебник Чистякова В.П. «Курс теории вероятностей»).

Замечание. Отметим, что запись не совсем корректна: если предельную случайную величину заменить на любую другую случайную величину 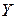с тем же законом распределения, то ничего не изменится, в том же смысле и . Поэтому слабая сходимость все же не есть сходимость последовательности случайных величин и ей нельзя пользоваться как сходимостями по вероятности, почти наверное и в среднем, для которых предельная случайная величина единственна (хотя бы с точностью до значений на множестве нулевой вероятности). По этой причине слабая сходимость и рассматривается отдельно.

Следующее утверждение устанавливает соотношение между слабой сходимостью и сходимостью по вероятности.

Лемма.

1. Из сходимости по вероятности следует слабая сходимость:

если , то .

2. Если предельное распределение является вырожденным, то сходимость по вероятности и слабая сходимость эквивалентны:

если , то .

▲ 1. Пусть - точка непрерывности функции распределения 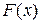. Требуется доказать, что тогда . Зафиксируем 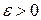такое, что 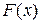непрерывна в точках .

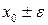Функцию распределения можно записать в виде:

.

Оценим вероятность сверху и снизу. Для вероятности 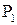имеем:

и вероятность справа может быть выбором 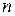сделана сколь угодно малой, поскольку .

Для вероятности 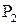, с одной стороны,

(так как, если , то тем более ).

С другой стороны,

(здесь первое неравенство очевидно, а второе следует из того, что ).

Таким образом, получаем для следующее двойное неравенство:

.

Устремляя теперь 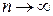, получаем

,

а предельный переход при с учетом того, что - точка непрерывности 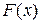, дает .

2. Пусть 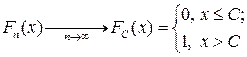для любого 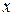, являющегося точкой непрерывности предельной функции распределения , то есть при всех .

Докажем, что при этом для любого .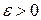

Раскроем модуль под знаком вероятности и выполним ряд преобразований:

,

поскольку в точках и функция распределения непрерывна. Окончательно, сходимость следует из леммы о двух милиционерах ■.

Замечательный факт состоит в том, что слабая сходимость распределений полностью характеризуется с помощью характеристических функций.

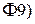Теорема непрерывности (без доказательства).

Пусть 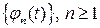- последовательность характеристических функций, а 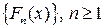- последовательность соответствующих функций распределений. Для слабой сходимости 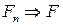необходимо и достаточно, чтобы для любого 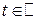, где 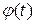- характеристическая функция, соответствующая предельной функции распределения .

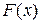Теорема непрерывности устанавливает, что соответствие между функциями распределения и характеристическими функциями является не только взаимнооднозначным (в соответствии с теоремой единственности), но и непрерывным в том смысле, что пределу в классе функций распределения относительно слабой сходимости соответствует предел в классе характеристических функций относительно поточечной сходимости.

Теорема непрерывности является основным средством доказательства центральных предельных теорем (теорем о слабой сходимости распределений на числовой прямой).

Дата добавления: 2015-06-30; просмотров: 346; Нарушение авторских прав

Мы поможем в написании ваших работ!