
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Понятие об усиленном законе больших чисел
Требование конечности дисперсии в законе больших чисел для независимых одинаково распределенных случайных величин (см. Теорему 3) связано исключительно со способом доказательства и в действительности это утверждение остается справедливым, если требовать только существование математического ожидания.
Теорема (Хинчина).
Любая последовательность 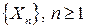 независимых одинаково распределенных случайных величин, имеющих конечное математическое ожидание
независимых одинаково распределенных случайных величин, имеющих конечное математическое ожидание 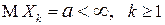 , подчиняется закону больших чисел, то есть
, подчиняется закону больших чисел, то есть
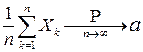 .
.
▲ Так как сходимость по вероятности к константе эквивалентна слабой сходимости (см. лемму о связи слабой сходимости со сходимостью по вероятности), то достаточно доказать слабую сходимость
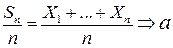 .
.
По теореме непрерывности 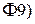 эта сходимость имеет место, если и только если для любого
эта сходимость имеет место, если и только если для любого 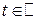
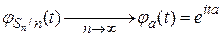 .
.
Вычислим характеристическую функцию случайной величины 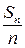 .
.
Пользуясь свойствами 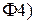 и
и 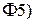 характеристических функций, имеем:
характеристических функций, имеем:
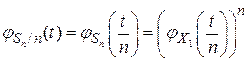 .
.
Поскольку первый момент случайной величины 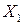 существует, то
существует, то 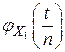 можно разложить в ряд Тейлора в окрестности нуля:
можно разложить в ряд Тейлора в окрестности нуля:
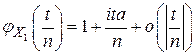
и, следовательно,
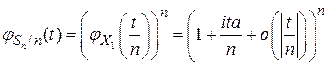 .
.
При 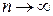 , пользуясь вторым замечательным пределом
, пользуясь вторым замечательным пределом 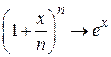 , имеем:
, имеем:
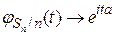 ■.
■.
В условиях теоремы Хинчина имеет место не только сходимость по вероятности 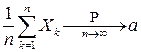 , но и сходимость почти наверное.
, но и сходимость почти наверное.
Теорема (Усиленный закон больших чисел Колмогорова для независимых одинаково распределенных случайных величин, без доказательства).
Если 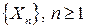 - последовательность независимых одинаково распределенных случайных величин, имеющих конечное математическое ожидание
- последовательность независимых одинаково распределенных случайных величин, имеющих конечное математическое ожидание 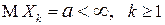 , то имеет место сходимость
, то имеет место сходимость
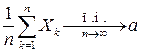
| <== предыдущая страница | | | следующая страница ==> |
| Центральная предельная теорема | | | Суббота, 21 марта 2015 |
Дата добавления: 2015-06-30; просмотров: 252; Нарушение авторских прав

Мы поможем в написании ваших работ!