Передаточная функция регулятора

Рациональные законы управления в каждом конкретном случае определяются желаемыми показателями качества процесса регулирования, технологическими требованиями с учетом ограничений на регулируемые параметры, энергетическими возможностями элементов и устройств системы регулирования и другими. Эти факторы в совокупности с возмущениями являются определяющими при выборе структуры контуров и расчете параметров системы подчиненного регулирования. Структура регуляторов зависит от структуры подобъекта и ограничений, и расчет параметров системы подчиненного регулирования по сути свой сводится к последовательной оптимизации всех соподчиненных контуров регулирования. В данном случае под оптимизацией понимается приведение передаточной функции контура регулирования в соответствие с поставленными требованиями.

В общем случае передаточную функцию объекта регулирования в любом из замкнутых контуров системы подчиненного регулирования можно представить в следующем виде

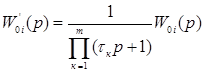. (7.2)

В том выражении второй сомножитель W_0i(p) – передаточная функция звеньев, определяющих инерционность объекта контура регулирования, т.е. звеньев с большими постоянными времени, а первый сомножитель – это произведение передаточных функций эквивалентных апериодических звеньев с малыми постоянными времени и существенно не влияющих на динамические свойства объекта.

Исходя из такой структуры объекта регулирования суть оптимизации любого соподчиненного контура регулирования заключается в компенсации больших постоянных времени и достижении, с учетом малых постоянных времени, требуемых динамических свойств замкнутого контура за счет соответствующих структуры и параметров регулятора.

Остановимся подробнее на вопросе компенсации постоянных времени объекта регулирования. Рассмотрим простейший случай, когда объект регулирования представляет собой апериодическое звено первого порядка

, (7.3)

где К и Т – соответственно коэффициенты усиления и постоянная времени звена.

Очевидно, что полная компенсация постоянной времени, т.е. трансформации апериодического звена в безинерционное (усилительное),? регулятор включенный последовательно с объектом должен иметь передаточную функцию

. (7.4)

Исходя из этого, передаточные функции разомкнутого и замкнутого контура регулирования соответственно равны

, (7.5)

. (7.6)

Контур регулирования получился безинерционным статическим.

Физически это означает, что для мгновенного изменения выходного параметра инерционного звена на его вход необходимо подать сигнал в виде импульса с бесконечно большой амплитудой, что реально невозможно ввиду ограниченности энергетических возможностей регулятора. В связи с этим абсолютная

компенсация инерционности технически невозможна, и можно говорить только о степени приближения к абсолютной компенсации. Однако по мере приближения к абсолютной компенсации снижается помехозащищенность контура регулирования.

Таким образом, предел приближения к абсолютной компенсации ограничивается энергетическими возможностями элементов и устройств системы регулирования и требованиями помехозащищенности отдельных контуров и системы регулирования в целом.

Ограничения предельного быстродействия в рассматриваемом случае можно достичь введением в контур регулирования фиктивного интегрирующего звена с постоянной времени Т₀ за счет регулятора. Тогда передаточная функция регулятора примет следующий вид:

. (7.7)

Соответственно передаточные функции разомкнутого и замкнутого контуров, согласно (7.5) и (7.6), равны

; (7.8)

. (7.9)

В этом случае замкнутый контур обращается в апериодическое звено, а статическая ошибка замкнутого контура сводится к нулю. Постоянную времени Т₀ в дальнейшем будем называть постоянной интегрирования контура.

Результатом компенсации в рассмотренном случае явилась замена разомкнутого контура интегрирующим звеном с постоянной интегрирования Т₀, а замкнутого контура апериодическим звеном с постоянной времени Т₀ и коэффициентом усиления равным единице.

В любом случае структура (передаточная функция) регулятора определяется структурой (передаточной функцией) объекта компенсации . При этом, в зависимости от вида передаточной функции, получается в основном три типа регуляторов.

Если объектом является интегрирующее звено

, (7.10)

то передаточная функция регулятора, из условия компенсации Т_и , равна

. (7.11)

В этом случае регулятор называется пропорциональным (П-регулятор).

Если объектом является инерционное звено первого порядка

, (7.12)

то передаточная функция регулятора равна

. (7.13)

В этом случае передаточная функция регулятора включает две составляющие – пропорциональную и интегральную, в соответствии с чем, регулятор называется пропорционально-интегральным (Пи-регулятор).

Если объектом является звено второго порядка

, (7.14)

то передаточная функция регулятора равна

. (7.15)

В этом случае передаточная функция регулятора включает три составляющие, в соответствии с чем, регулятор называется пропорционально-интегрально-дифференциальным (ПИД-регулятор). Независимо от структуры объекта, при изложенном принципе выбора регулятора передаточные функции разомкнутого и замкнутого контуров соответственно равны

; (7.16)

. (7.17)

Таким образом, на основании изложенного выше, можно заключить, что в результате точной компенсации постоянных времени объекта регулирования, независимо от его структуры, и введения в контур регулирования, за счет регулятора, фиктивного интегрирующего звена, передаточная функция и параметры разомкнутого и замкнутого контуров описываются выражениями (7.16) и (7.17).

Рис. 7.2. Структурные схемы контура регулирования: а – исходная; б – преобразованная.

Реальные объекты регулирования в общем случае могут включать в себя звенья как с большими, так и с малыми постоянными времени, как показано на рис. 7.2а. Если и параметры регулятора выбраны из условия компенсации больших постоянных времени, входящих в W_ок(р), то структурная схема контура регулирования принимает вид, представленный на рис. 7.2б, и передаточная функция разомкнутого контура равна

. (7.18)

При без существенной погрешности, пренебрегая членами высшего порядка можно принять

, (7.19)

где - сумма малых постоянных времени объектов регулирования в контуре.

Тогда

(7.20)

и соответственно для замкнутой

. (7.21)

Принимая, что в общем случае

, (7.22)

для разомкнутого и замкнутого контуров передаточные функции равны

; (7.23)

. (7.24)

В этих выражениях коэффициент а определяет быстродействие контура регулирования и называется коэффициентом демпфирования. В конечном итоге все контуры регулирования можно представить эквивалентным инерционным звеном второго порядка с передаточной функцией (7.24).

С учетом вышепринятого допущения структурная схема любого контура системы подчиненного регулирования может быть представлена в виде приведенном на рис. … . Согласно этой структурной схеме передаточная функция разомкнутого контура запишется в следующем виде

. (7.25)

Тогда, из условия равенства правых частей (7.24) и (7.25) получим выражение для определения передаточной функции регулятора

. (7.26)

Дата добавления: 2015-06-30; просмотров: 228; Нарушение авторских прав

Мы поможем в написании ваших работ!