Понятие минтерма и макстерма булевой функции и их свойства

Минтермом (или элементарной конъюнкцией Q_i, или конституентой единицы) называется логическое произведение прямых или инверсных переменных, причем каждая переменная в произведении встречается только один раз: .

Макстермом (или элементарной дизъюнкцией D_i, или конституентой нуля) называется логическая сумма прямых или инверсных переменных, причем каждая переменная встречается в сумме только один раз: .

Количество минтермов и макстермов заданного числа аргументов совпадает с числом различных наборов аргументов N = 2ⁿ.

Свойства минтермов и макстермов:

1. Между индексами і одноименных минтермов и макстермов булевых n переменных существуют следующие соотношения: , , где индекс i – десятичное число и соответствует двоичному коду, отвечающему комбинации значений аргументов функции.

2. Логическая сумма всех минтермов любого числа переменных равна единице.

3. Логическое произведение всех макстермов любого числа переменных равно нулю.

4. Логическое произведение минтермов, имеющих разные индексы, равно нулю, т.e. Q_i·Q_j=0, при i ? j.

5. Логическая сумма неодинаковых макстермов равна единице, т.е. D_i+D_j=1, при i ? j.

Для построения СДНФ логической функции F_CDHФ от n переменных, заданной таблицей истинности, необходимо по каждому набору переменных, на котором функция принимает значение 1, записать конъюнкцию – минтерм вида и все такие конъюнкции соединить знаками дизъюнкции. При этом переменные, имеющие значение нуля, инвертируются , , ,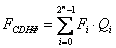где i – десятичные числа, соответствующие тем наборам аргументов, на которых F=F_i=1.

Для построения СКНФ логической функции F_CКHФ от n переменных, заданной таблицей истинности, необходимо по каждому набору переменных, на котором функция принимает значение 0, записать дизъюнкцию – макстерм вида 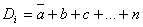и все такие дизъюнкции соединить знаками конъюнкции. При этом переменные, имеющие значение единицы, инвертируются: 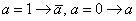, , где i – десятичные числа, соответствующие тем наборам аргументов, на которых F=F_i=0.

Дата добавления: 2015-07-26; просмотров: 258; Нарушение авторских прав

Мы поможем в написании ваших работ!