Синтез схем в базисе функции Пирса

Основой для получения минимальных форм логических функций в базисах функций

штрих Шеффера и стрелка Пирса может служить МДНФ, полученная в результате

решения задачи минимизации.

МДНФ представляет собой дизъюнкцию простых импликант и может быть

представлена в обобщенном виде:

(1)

где Ji – символ импликант, а d - их количество.

Формулы функций штрих Шеффера и стрелка Пирса для случая r переменных имеют вид:

(2)

(3)

Для перехода от МДНФ к минимальной форме в базисе функции штрих Шеффера

конъюнкции и дизъюнкции в выражении (1) должны быть заменены функциями вида

(2). Это достигается двукратным инвертированием (1) и применением теоремы де

Моргана-Шеннона. Первое инвертирование (1) с учетом указанной теоремы

приводит к соотношению:

(4)

Второе инвертирование с учетом закона двойного отрицания дает:

(5)

Каждый из членов

соотношения (5) и все это соотношение в целом представляет собой функции штрих

Шеффера.

Следовательно, (5) выражает переход от МДНФ к искомой форме формулы в базисе

функций штрих Шеффера. Формулу (5) называют оптимальной конъюнктивной

инверсной формой логической функции или оптимальным инверсным

произведением.

Переход от МДНФ к минимальной форме в базисе функций стрелка Пирса

осуществляется заменой импликант в (1) функциями вида (3). Обозначим

преобразованную в соответствии с теоремой де Моргана-Шеннона инверсию

импликанты

символом Gi. Тогда (4) можно переписать в виде:

(6)

Трехкратное инвертирование (6) приводит к искомой форме формулы в базисе

функций стрелка Пирса

(7)

Каждый член дизъюнкции в (7) и инверсия всей дизъюнкции представляет собой

функции стрелка Пирса; заключительное инвертирование также может быть выполнено

элементами стрелка Пирса (ИЛИ - НЕ). Формулу (7) называют оптимальной

дизъюнктивной инверсной формой логической функции или оптимальной

инверсной суммой.

Пример. 6. Представить логическую функцию «равнозначность двух

переменных» в базисе функций штрих Шеффера и стрелка Пирса.

Решение. СДНФ функции равнозначность двух переменных (приведена выше) имеет вид:

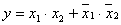(8)

Первое инвертирование (8) с учетом теоремы де Моргана приводит к выражению:

.

Второе инвертирование с учетом закона двойного отрицания приводит к искомой

форме в базисе функций штрих Шеффера:

(8.1)

Четырехкратное инвертирование (8.1) дает искомую форму в базисе функций

стрелка Пирса:

Дата добавления: 2015-07-26; просмотров: 450; Нарушение авторских прав

Мы поможем в написании ваших работ!