Принципы склейки

• Склейку клеток карты Карно можно осуществлять по единицам (если необходимо получить ДНФ) или по нулям (если требуется КНФ).
• Склеивать можно только прямоугольные области с числом единиц (нулей) 2ⁿ, где n — целое число. Для карт Карно с числом переменных более четырёх могут получаться более сложные области, о чём будет сказано в следующих разделах.
• Область, которая подвергается склейке должна содержать только единицы (нули).
• Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой (топологически карта Карно для четырёх переменных представляет собой тор) и могут объединяться в прямоугольники. Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули) они могут быть объединены в квадрат, как показано на рис. 2в.
• Все единицы (нули) должны попасть в какую-либо область.
• С точки зрения минимальности ДНФ (КНФ) число областей должно быть как можно меньше (каждая область представляет собой терм), а число клеток в области должно быть как можно больше (чем больше клеток в области, тем меньше переменных содержит терм. Терм размером 2ⁿ ячеек содержит N–n переменных).
• Одна ячейка карты Карно может входить сразу в несколько областей. Это следует из очевидного свойства булевых функций: повторение уже существующего слагаемого (сомножителя) не влияет на функцию:

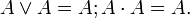
• В отличие от СДНФ (СКНФ), ДНФ (КНФ) не единственны. Возможно несколько эквивалентных друг другу ДНФ (КНФ), которые соответствуют разным способам покрытия карты Карно прямоугольными областями.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

1. Объединяем смежные клетки, содержащие единицы, в область так, чтобы одна область содержала 2ⁿ (n целое число = 0… ) клеток (помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули;
2. Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
3. Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну;
4. Область должна быть как можно больше, а количество областей как можно меньше;
5. Области могут пересекаться;
6. Возможно несколько вариантов покрытия.

Далее берём первую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.

Для КНФ всё то же самое, только рассматриваем клетки с нулями, неменяющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной.

Дата добавления: 2015-07-26; просмотров: 145; Нарушение авторских прав

Мы поможем в написании ваших работ!