
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Дифференциальные уравнения, допускающие понижение порядка
Укажем некоторые виды дифференциальные уравнений, допускающих понижение порядка.
I. Уравнение вида  . После n-кратного интегрирования получается общее решение
. После n-кратного интегрирования получается общее решение
II. Уравнение не содержит искомой функции и её производных до порядка  включительно:
включительно:

Порядок такого уравнения можно понизить на  единиц заменой
единиц заменой  . Тогда уравнение примет вид
. Тогда уравнение примет вид

Из последнего уравнения, если это возможно, определяем  , а затем находим
, а затем находим  из уравнения
из уравнения  k-кратным интегрированием.
k-кратным интегрированием.
III. Уравнение не содержит независимого переменного:

Подстановка  позволяет понизить порядок уравнения на единицу. При этом
позволяет понизить порядок уравнения на единицу. При этом  рассматривается как новая неизвестная функция от
рассматривается как новая неизвестная функция от  . Все производные
. Все производные  выражаются через производные от новой неизвестной функции
выражаются через производные от новой неизвестной функции  по
по 
Подставив эти выражения вместо  в уравнение, получим дифференциальное уравнение (n–1)-го порядка.
в уравнение, получим дифференциальное уравнение (n–1)-го порядка.
IV. Уравнение  , однородное относительно аргументов
, однородное относительно аргументов  , т.е.
, т.е.

Порядок такого уравнения может быть понижен на единицу подстановкой  , где
, где  — новая неизвестная функция от
— новая неизвестная функция от  .
.
V. Уравнение, записанное в дифференциалах,

в котором функция  однородна относительно своих аргументов
однородна относительно своих аргументов  , если считать
, если считать  и
и  — первого измерения, а
— первого измерения, а  и т.д. — измерения
и т.д. — измерения  . Тогда
. Тогда  будет иметь измерение
будет иметь измерение  ,
,  – измерение
– измерение  и т.д.
и т.д.
Для понижения порядка применятся подстановка  . В результате получается дифференциальное уравнение между
. В результате получается дифференциальное уравнение между  и
и  , не содержащее явно
, не содержащее явно  , т. е допускающее понижение порядка не единицу (случай III).
, т. е допускающее понижение порядка не единицу (случай III).
Рассмотрим примеры на различные случаи понижения порядка дифференциального уравнения.
Пример 1. Найти общее решение уравнения  .
.
Решение. Интегрируя последовательно данное уравнение, имеем:
Пример 2. Найти общее решение уравнения  и выделить решение, удовлетворяющее начальным условиям
и выделить решение, удовлетворяющее начальным условиям  .
.
Решение. Интегрируем это уравнение последовательно три раза:
| (1) |
Найдем решение, удовлетворяющее заданным начальным условиям. Подставляя начальные данные  в (1), будем иметь систему трёх уравнений
в (1), будем иметь систему трёх уравнений

Отсюда  . Искомым решением будет
. Искомым решением будет

Пример 3. Решить дифференциальное уравнение третьего порядка  .
.
Решение. Данное уравнение не содержит искомой функции  и ее производной, поэтому полагаем
и ее производной, поэтому полагаем  . После этого уравнение примет вид
. После этого уравнение примет вид

Разделяя переменные и интегрируя, найдем

Заменим  на
на  , получим
, получим  .
.
Интегрируя последовательно, будем иметь
 и
и 
или

Пример 4. Решить уравнение пятого порядка  .
.
Решение. Уравнение не содержит искомой функции и ее производных до третьего порядка включительно. Поэтому, полагая  , получаем
, получаем
 откуда
откуда 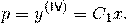
Последовательно интегрируя, найдем
или  , где .
, где .
Пример 5. Решить уравнение  .
.
Решение. Уравнение не содержит независимого переменного  . Полагая
. Полагая  получаем уравнение Бернулли
получаем уравнение Бернулли

Подстановкой  оно сводится к линейному уравнению
оно сводится к линейному уравнению
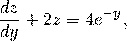
общее решение которого  . Заменяя
. Заменяя  на
на  , получаем
, получаем

Разделяя переменные и интегрируя, будем иметь
 , откуда
, откуда 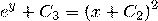 , где
, где  .
.
Это и есть общий интеграл исходного дифференциального уравнения.
Пример 6. Решить уравнение  .
.
Решение. Данное уравнение однородно относительно  . Порядок этого уравнения понижается на единицу подстановкой
. Порядок этого уравнения понижается на единицу подстановкой  , где
, где  — новая неизвестная функция от
— новая неизвестная функция от  . Имеем
. Имеем

Подставляя выражения для  в уравнение, получаем
в уравнение, получаем

Сокращаем на 
 , или
, или  .
.
Это уравнение линейное. Левую часть его можно записать в виде  , откуда
, откуда
 , или
, или  .
.
Находим интеграл:
Общим решением данного уравнения будет
 , или
, или  .
.
Кроме того, уравнение имеет очевидное решение  , которое получается из общего при
, которое получается из общего при  .
.
Пример 7. Решить уравнение  .
.
Решение. Покажем, что это уравнение — обобщенное однородное. Считая  величинами 1-го, m-го, (m–1)-го и (m–2)-го измерений соответственно и приравнивая измерения всех членов, получаем
величинами 1-го, m-го, (m–1)-го и (m–2)-го измерений соответственно и приравнивая измерения всех членов, получаем

| (2) |
откуда  . Разрешимость уравнения (2) является условием обобщенной однородности уравнения.
. Разрешимость уравнения (2) является условием обобщенной однородности уравнения.
Сделаем подстановку  . Так как
. Так как
то данное уравнение после сокращения на множитель  примет вид
примет вид

Положив  , получим
, получим  . Отсюда
. Отсюда  или
или  . Интегрируя второе уравнение, найдем
. Интегрируя второе уравнение, найдем
 , или
, или  .
.
Общее решение этого уравнения будет  . Возвращаясь к переменным
. Возвращаясь к переменным  и
и  , получаем общее решение данного уравнения
, получаем общее решение данного уравнения
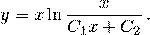
Случай  дает
дает  или
или  — частное решение, которое получается из общего при
— частное решение, которое получается из общего при  .
.
Замечание. При решении задачи Кош и для уравнений высших порядков целесообразно определять значения постоянных  в процессе решения, а не после нахождения общего решения уравнения. Это ускоряет решение задачи и, кроме того, может оказаться, что интегрирование значительно упрощается, когда постоянные
в процессе решения, а не после нахождения общего решения уравнения. Это ускоряет решение задачи и, кроме того, может оказаться, что интегрирование значительно упрощается, когда постоянные  принимают конкретные числовые значения, в то время как при произвольных
принимают конкретные числовые значения, в то время как при произвольных  интегрирование затруднительно, а то и вообще невозможно в элементарных функциях.
интегрирование затруднительно, а то и вообще невозможно в элементарных функциях.
Пример 8. Решить задачу Коши  .
.
Решение. Полагая  , получаем
, получаем  откуда
откуда
 , или
, или  .
.
Разделяя переменные, найдем

В правой части последнего равенства имеем интеграл от дифференциального бинома. Здесь 
 и
и  , т.е. неинтегрируемый случай.
, т.е. неинтегрируемый случай.
Следовательно, этот интеграл не выражается в виде конечной комбинации элементарных функций. Однако если использовать начальные условия, то получим  . Так что
. Так что  , откуда, учитывая начальные условия, окончательно находим
, откуда, учитывая начальные условия, окончательно находим  .
.
Пример 9. Найти плоские кривые, у которых радиус кривизны пропорционален длине нормали.
Решение. Пусть  — уравнение искомой кривой. Ее радиус кривизны
— уравнение искомой кривой. Ее радиус кривизны  . Длина нормали
. Длина нормали  кривой равна (рис.24):
кривой равна (рис.24):  .
.
Определяющее свойство кривой выражается дифференциальным уравнением

| (3) |
где  — коэффициент пропорциональности, могущий принимать как положительные, так и отрицательные значения. Перепишем уравнение (3) в виде
— коэффициент пропорциональности, могущий принимать как положительные, так и отрицательные значения. Перепишем уравнение (3) в виде

Интегрируя, находим
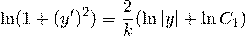 , или
, или  .
.
Разделяя переменные и интегрирую еще раз, получаем

общий интеграл исходного уравнения (3). Рассмотрим некоторые частные случаи.
1)  . Тогда будем иметь
. Тогда будем иметь 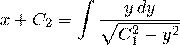 , и после интегрирования
, и после интегрирования  . Отсюда получаем
. Отсюда получаем  . Искомые кривые — окружности произвольных радиусов с центрами на оси
. Искомые кривые — окружности произвольных радиусов с центрами на оси  .
.
2)  . В этом случае приходим к уравнению
. В этом случае приходим к уравнению

Полагая  , найдем, что
, найдем, что  . Таким образом, искомые кривые определяются в параметрической форме уравнениями:
. Таким образом, искомые кривые определяются в параметрической форме уравнениями:

Это — циклоиды, образованные качение по оси  окружностей произвольных радиусов.
окружностей произвольных радиусов.
3)  . В этом случае имеем
. В этом случае имеем
откуда
Складывая полученные равенства, будем иметь
это — цепные линии.
4)  . Тогда будем иметь
. Тогда будем иметь
 , или
, или  .
.
Отсюда  ; это — параболы, оси которых параллельны оси ординат
; это — параболы, оси которых параллельны оси ординат  .
.
| <== предыдущая страница | | | следующая страница ==> |
| | | C. Синдром Таласа-Ханта |
Дата добавления: 2015-07-26; просмотров: 314; Нарушение авторских прав

Мы поможем в написании ваших работ!