Непрерывность функции на интервале

Определение :

Пусть f - некоторая функция, D(f)- ее область определения и 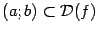- некоторый (открытый) интервал ( может быть 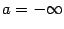или 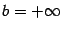) Назовём функцию 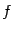непрерывной на интервале 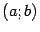, если 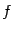непрерывна в любой точке 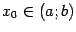, то есть для любого 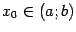существует 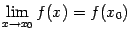(в сокращённой записи:

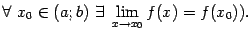
Свойства непрерывных функций

Теорема 1. Сумма непрерывных функций есть функция непрерывная.

Доказательство. Пусть функци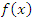и и непрерывны в точке a. Тогда

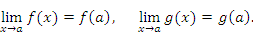
Согласно свойству пределов функций существование пределов функци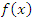й и гарантирует существование предела их суммы. При этом

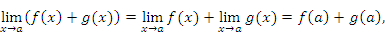
что и требовалось доказать.

Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная.

Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция.

Теорема 2. Произведение непрерывных функций есть функция непрерывная.

Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная.

Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль.

Теорема 4. Любая элементарная функция непрерывна в области своего определения.

Для доказательства этой теоремы нужно показать, что для любого числа a из области определения элементарной функции 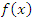выполняется условие

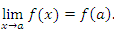
Продемонстрируем справедливость теоремы на некоторых конкретных примерах.

1. Пусть 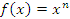, где n – целое положительное число. Тогда

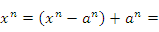
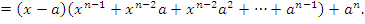
Первый член в правой части этого равенства представляет собой бесконечно малую функцию при x → a и, следовательно,

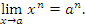
1. Покажем, что показательная функция 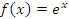является непрерывной в каждой точке a. Действительно,

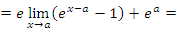
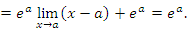
Теорема 5. Пусть функция 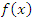непрерывна на промежутке [a,b] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка c, в которой .

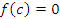Действительно, непрерывность функции на некотором промежутке означает отсутствие скачков функции на этом промежутке. Другими словами, 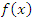принимает все значения, заключенные между ее минимальным и максимальным значениями на промежутке [a,b], одним из которых является нулевое значение.

Дата добавления: 2015-07-26; просмотров: 227; Нарушение авторских прав

Мы поможем в написании ваших работ!