Интегрирование рациональных функций

Функция, заданная в виде

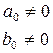(1)

называется рациональной функцией.

Если 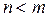, то дробь правильная, при - дробь неправильная.

I. Метод интегрирования правильной рациональной дроби состоит в разложении этой дроби на простейшие. При этом следует пользоваться следующим правилом:

а) каждому простому действительному корню а знаменателя соответствует одно слагаемое в разложении:

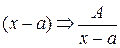(2)

б) каждому действительному корню b кратности k знаменателя соответствует сумма k - слагаемых:

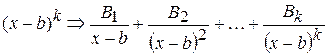(3)

в) каждому сомножителю 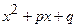знаменателя, неимеющему действительных корней, соответствует слагаемое:

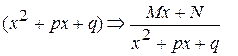(4)

г) каждому сомножителю 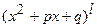знаменателя, неимеющему действительных корней ,соответствует сумма слагаемых:

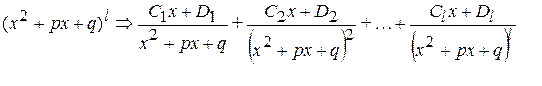(5)

Таким образом

(6)

Числа 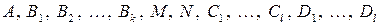могут быть найдены с помощью метода неопределенных коэффициентов. Для этого необходимо:

1) привести к общему знаменателю сумму дробей, стоящую в правой части (6);

2) приравнять числитель полученной дроби к ;

3) приравнять коэффициенты при одинаковых степенях x в полученном в п.2 равенстве;

4) решить полученную систему линейных уравнений относительно неизвестных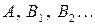

Числа 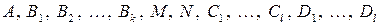также могут быть найдены с помощью метода частных значений. Для этого необходимо

придавая переменной 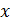разлчные частные значения, получить значения неопределенных коэффициентов.

Из (6) видно, что вычисление интеграла от правильной рациональной функции сводится к вычислению одного из интегралов вида:

а) ;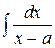

б) ;

в) ;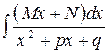

г) .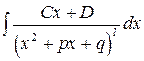

II. Интегрирование неправильной рациональной дроби начинается с представления ее в виде суммы многочлена и правильной рациональной дроби путем деления числителя на знаменатель.

Таким образом, интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.

Итак, общее правило интегрирования рациональных дробей:

1. Если дробь неправильная, то представить её в виде суммы многочлена и правильной дроби.

2. Разложить знаменатель правильной рациональной дроби на множители.

3. Представить дробь в виде суммы простейших рациональных дробей.

4. Найти неизвестные коэффициенты способом сравнения соответствующих коэффициентов или способом частных значений (см. пример ниже).

5. Проинтегрировать многочлен и полученную сумму простейших дробей.

Дата добавления: 2015-07-26; просмотров: 176; Нарушение авторских прав

Мы поможем в написании ваших работ!