
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Процент. Основные задачи на проценты
1º. Процентом называется сотая часть какого-либо числа. Следовательно, само число составляет 100 процентов. Слово «процент» заменяют знаком %, т.е. 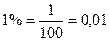 .
.
2º. При решении основных задач на проценты (нахождение процентов данного числа; нахождение числа по его процентам) некоторая величина b принимается за 100 %, а ее часть – величина a – принимается за p % и составляется пропорция
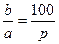 .
.
Из этой пропорции по двум известным величинам определяют искомую третью величину, пользуясь основным свойством пропорции: b · p = 100 · a .
Пример 2. Сколько процентов числа 7 составляет разность между ним и 4 % числа 28?
Решение.
Найдем 4 % от числа 28. Чтобы найти проценты от числа, надо перевести проценты в десятичную дробь и умножить данное число на эту дробь. Это будет: 28 · 0,04 = 1,12.
Определим разность 7 – 1,12 = 5,88. Найдем, сколько процентов числа 7 составляет 5,88. Для этого составим пропорцию:
число 7 – 100 %,
число 5,88 – x %.
Отсюда 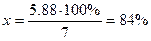 .
.
3º. Чтобы найти процентное отношение двух чисел a и b, надо отношение этих чисел умножить на 100%, т.е. вычислить 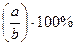 .
.
4º. При нахождении суммы вклада в банк используют формулу простых процентов или формулу сложных процентов.
Простой процентный рост: 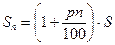 , где S – начальная сумма вклада, p - число процентов годовых, n – срок вклада,
, где S – начальная сумма вклада, p - число процентов годовых, n – срок вклада,  - величина вклада через n лет.
- величина вклада через n лет.
Сложный процентный рост: 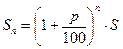 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Десятичные дроби. Действия над десятичными дробями | | | Дидактический материал. а) 40% его равны 12; б) 1,25 % его равны 55; в) 0,8% его равны 1,84; г) % его равны |
Дата добавления: 2015-07-26; просмотров: 233; Нарушение авторских прав

Мы поможем в написании ваших работ!