Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Лекция № 19. Тема 4 : Производная и дифференциал
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
4.1. Производная функции
Пусть функция 
определена в точке х и некоторой её окрест-ности 
.
Определение 1. Производной от функции в точке х называется предел отношения её приращения 
в этой точке к соответствующему приращению аргумента 
при 
и обозначается
. 
(1)
Другие обозначения производной: 
Замечание 1. Очевидно для существования предела (1) необходимо вы-полнение равенства 
, где 
- левая производ-ная ( 
), а 
- правая производная ( 
).
Определение 2. Функция , имеющая конечную производную в точке х, называется дифференцируемой в этой точке, а если она диффе-ренцируемая в каждой точке промежутка 
, то она называется диффе-ренцируемой в этом промежутке.
Замечание 2. Не для всех функций существует предел (1).
Например, определим производную функции 
в точке 
раскроем знак модуля, вычисляя предел (1) слева и справа,
Таким образом, функция является не дифференцируемой в точке 
Пример показывает, что не всякая непрерывная функция является дифференцируемой. Верно ли обратное?
Теорема 1. Если функция 
дифференцируемая в некоторой точке x, то она непрерывна в этой точке.
Пусть существует предел (1). Это по теореме о пределе функции означает, что
, где 
. (2)
Из формулы (2) следует 
. Переходя к пределу, получаем
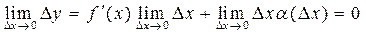, ч.т.д.
Обратное, вообще говоря, неверно (например, функция ).
4.2. Производные основных элементарных функций
Используя определение производной, можно получить значения производных основных элементарных функций. Рассмотрим примеры:
Пример 1. Найти производную функцию 
.
.
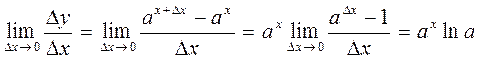При вычислении предела мы использовали Пример 5 из Лекции 17.
В частности, если 
, то 
.
Пример 2. Аналогично, для функции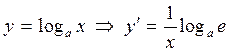 
.
В частности, если 
Пример 3. Найти производную функции 
.
Пример 4. Аналогично, для функции 
.
Приведём таблицу производных элементарных функций:
1. 
.
2. 
. 3. 
.
4. 
. 5. 
.
6. 
. 7. .
8. 
. 9. 
.
10. 
. 11. 
.
12. 
. 13. 
.
Формулы (2-7) нами доказаны.
Остальные формулы будут доказаны позже.
4.3. Механический смысл производной
Рассмотрим прямолинейное движение точки М. Пусть в момент времени t точка М находится на расстоянии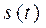 
от начального поло-жения М0.
t0 t 
s
М0 М М1
В последующий момент точка М заняла положение М1 на расстоянии 
от начального положения. Тогда средняя скорость за 
будет 
, а скорость 
в момент времени t :
.
Таким образом, если функция 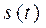– это путь, проходимый точкой М, то производная 
от этой функции – скорость движения точки.
4.4. Геометрический смысл производной
Пусть функция дифференцируема в точке х.
у 
О х 
х
Из рисунка следует, что 
.Перейдём к пределу при 
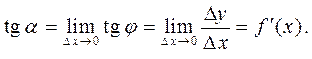
Таким образом, значение производной равно тангенсу угла наклона касательной, проведённой в данной точке. Исходя из этого, уравнение касательной в точке 
к кривой имеет вид
.
Прямая, проходящая через точку М0, перпендикулярно касательной называется нормалью. Её уравнение имеет вид
.
Отметим частный случай:
если 
- уравнение касательной, 
- нормали.
Пример 6. Найти уравнения касательной и нормали к функции 
в точке 
Имеем 
Найдем производную функции
Таким образом, получим
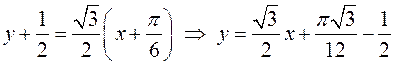- уравнение касательной,
- уравнение нормали.
4.5. Правила дифференцирования
Пусть функции U(х)и V(х) дифференцируемые.
1. Если 
.
2. 
.
3. 
.
4. 
.
Докажем последнее правило
.
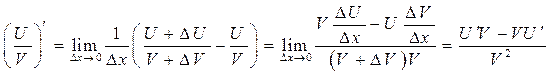Пример 5. Найти производные функций 
и 
.
.
Аналогично, 
,
т.е. доказаны формулы (8-9) таблицы производных.
4.6. Производная сложной функции
Пусть дана сложная функция 
, т.е. 
Теорема 2. Если функция 
имеет в точке x производную 
, а функция 
в соответствующей точке и также имеет производную 
, то сложная функция 
в точке х имеет производную, которая равна
.
По условию теоремы существует 
. По теореме о пре-деле функции из существования этого предела следует
,
где 
или
. (3)
Разделим выражение (3) на 
. (4)
Переходя к пределу в формуле (4) при 
, а тогда в силу непрерывности и 
, получим
. (5)
Замечание 3. Формулу (5) можно обобщить для любого числа суперпозиций функций. Например, если
.
Пример 7. Найти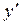 
, если 
.
.
Пример 8. Найти 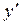, если 
Представим 
и по правилу дифференцирования сложной функции получим
,
т.е. доказана и первая формула из таблицы производных.
| <== предыдущая страница | | | следующая страница ==> |
| | | Тема: Методы вычисления определенного интеграла |
Дата добавления: 2015-07-26; просмотров: 226; Нарушение авторских прав
Мы поможем в написании ваших работ!