
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Дифференциальные уравнения второго порядка
Дифференциальным уравнением второго порядка называется уравнение вида:
 ,
,
где  - независимая переменная,
- независимая переменная,  - искомая функция, первая и вторая ее производные.
- искомая функция, первая и вторая ее производные.
Теорема Коши о существовании и единственности решения дифференциального уравнения второго порядка. Пусть функция  и ее частные производные
и ее частные производные 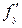 и
и  непрерывны в некоторой области
непрерывны в некоторой области  пространства переменных
пространства переменных  . Тогда для любой внутренней точки
. Тогда для любой внутренней точки  этой области существует единственное решение уравнения
этой области существует единственное решение уравнения  удовлетворяющее условиям
удовлетворяющее условиям  .
.
Условия  называются начальными условиями, а задачу отыскания решения уравнения
называются начальными условиями, а задачу отыскания решения уравнения  по заданным начальным условиям
по заданным начальным условиям  называют задачей Коши.
называют задачей Коши.
Пример. Найти решение задачи Коши:  .
.
Решение: Найдем общее решение:
 .
.
Воспользуемся начальными условиями и найдем частное решение:
 .
.
Ответ:  - решение задачи Коши.
- решение задачи Коши.
Типы дифференциальных уравнений второго порядка:
1. Уравнения, допускающие понижение порядка, бывают трех видов:
А)  . Для решения используется замена:
. Для решения используется замена:  , тогда
, тогда  , а
, а  .
.
Б)  . В этом случае замена имеет вид:
. В этом случае замена имеет вид:  , тогда
, тогда  , а
, а  .
.
В)  . Замена:
. Замена:  . Тогда
. Тогда  , а общее решение можно представить в виде:
, а общее решение можно представить в виде: 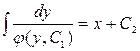 .
.
Пример. Найти решение уравнения:  .
.
Решение: В нашем случае  , следовательно, используем замену:
, следовательно, используем замену:  и получим уравнение с разделяющимися переменными
и получим уравнение с разделяющимися переменными
 .
.
Выполняем обратную замену:
 .
.
Ответ:  .
.
2. Линейное дифференциальное уравнение второго порядка – это уравнение вида:  , где
, где  - искомая функция,
- искомая функция,  - известные непрерывные функции на интервале
- известные непрерывные функции на интервале  . Если
. Если  , то уравнение называется линейным однородным дифференциальным уравнением. Если
, то уравнение называется линейным однородным дифференциальным уравнением. Если  , то линейным неоднородным дифференциальным уравнением.
, то линейным неоднородным дифференциальным уравнением.
А) Рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:  , где
, где 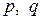 - вещественные числа.
- вещественные числа.
Линейное дифференциальное уравнение второго порядка имеет два базисных решения, по которым строится общее решение уравнения. Решения 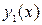 и
и  уравнения
уравнения  называются линейно независимыми, если их линейная комбинация равна нулю
называются линейно независимыми, если их линейная комбинация равна нулю  , лишь в том случае, когда
, лишь в том случае, когда 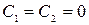 .
.
Теорема. Пусть решения 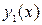 и
и  уравнения
уравнения  линейно независимы на интервале
линейно независимы на интервале  . Тогда функция
. Тогда функция  , где
, где  и
и  - произвольные постоянные, является общим решением однородного уравнения
- произвольные постоянные, является общим решением однородного уравнения  .
.
Решение уравнения  будем искать в виде
будем искать в виде  , где
, где  - некоторое число. Поставим эту функцию в уравнение и получим
- некоторое число. Поставим эту функцию в уравнение и получим  . Разделим обе части на
. Разделим обе части на  и будем иметь
и будем иметь  - это уравнение называется характеристическим уравнением для дифференциального уравнения
- это уравнение называется характеристическим уравнением для дифференциального уравнения  .
.
Вид общего решения  зависит от того какие корни
зависит от того какие корни  и
и  имеет характеристическое уравнение
имеет характеристическое уравнение  .
.
Теорема. Если корни характеристического уравнения:
· вещественные и различные, т.е.  , то общее решение однородного дифференциального уравнения имеет вид
, то общее решение однородного дифференциального уравнения имеет вид  .
.
· вещественные и равны между собой, т.е.  , то общее решение однородного дифференциального уравнения имеет вид
, то общее решение однородного дифференциального уравнения имеет вид 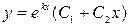 .
.
· комплексные  , где
, где  , а
, а  и
и  - вещественные числа, то общее решение однородного дифференциального уравнения имеет вид
- вещественные числа, то общее решение однородного дифференциального уравнения имеет вид 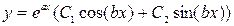 , где
, где  .
.
Во всех трех случаях  и
и  - произвольные постоянные.
- произвольные постоянные.
Пример. Найти общее решение: а)  ; б)
; б)  ; в)
; в) 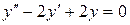 .
.
Решение:
а) Характеристическое уравнение имеет вид:  . Оно имеет два различных вещественных корня
. Оно имеет два различных вещественных корня  , следовательно
, следовательно  .
.
б) Характеристическое уравнение:  . Оно имеет два вещественных корня, равных между собой
. Оно имеет два вещественных корня, равных между собой  , тогда общее решение имеет вид
, тогда общее решение имеет вид  .
.
в) Характеристическое уравнение:  . В этом случае, мы имеет комплексные корни
. В этом случае, мы имеет комплексные корни  , следовательно,
, следовательно,  .
.
Ответ: а)  ; б)
; б)  ;
;
в)  .
.
Б) Неоднородные уравнения второго порядка – это уравнения вида  .
.
Общее решение  неоднородного дифференциального уравнения второго порядка состоит из суммы общего решения
неоднородного дифференциального уравнения второго порядка состоит из суммы общего решения  соответствующего однородного дифференциального уравнения
соответствующего однородного дифференциального уравнения  и некоторого частного решения
и некоторого частного решения  неоднородного дифференциального уравнения
неоднородного дифференциального уравнения  , т.е.
, т.е.  .
.
Вид частного решения  зависит от функции
зависит от функции  и корней характеристического уравнения:
и корней характеристического уравнения:
· Если 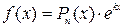 , где
, где  - многочлен степени
- многочлен степени  . Тогда
. Тогда  , где
, где 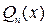 - многочлен степени
- многочлен степени  в общем виде, а
в общем виде, а 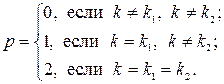
· Если 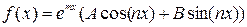 , где
, где  - заданные действительные числа. Тогда
- заданные действительные числа. Тогда  , где
, где  и
и  - неизвестные числа, а
- неизвестные числа, а  .
.
Пример. Найти решение уравнения:  .
.
Решение: Находим общее решение соответствующего однородного уравнения  , которое будет иметь вид:
, которое будет иметь вид: 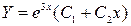 .
.
Частное решение будем искать виде  , тогда
, тогда  ,
,  . Подставляем в исходное уравнение:
. Подставляем в исходное уравнение:

Следовательно,  , а общее решение
, а общее решение  .
.
Ответ:  .
.
Пример. Найти решение задачи Коши:
 .
.
Решение: Находим общее решение соответствующего однородного уравнения  , которое будет иметь вид:
, которое будет иметь вид:  .
.
Частное решение будем искать виде  , тогда
, тогда  ,
,  . Подставляем в исходное уравнение:
. Подставляем в исходное уравнение: 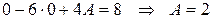 , т.е.
, т.е.  .
.
Общее решение уравнения получим в виде:  .
.
Найдем значение констант с помощью заданных начальных условий:

Ответ:  .
.
| <== предыдущая страница | | | следующая страница ==> |
| | | Задания для самостоятельной работы. Проверить, являются ли решением данных дифференциальных уравнений указанные функции |
Дата добавления: 2015-07-26; просмотров: 347; Нарушение авторских прав

Мы поможем в написании ваших работ!