
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Линейные дифференциальные уравнения 1-го порядка
Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:
 , (7.1)
, (7.1)
где P(x) и Q(x) – заданные непрерывные функции от x. Если функция  , то уравнение (7.1) имеет вид:
, то уравнение (7.1) имеет вид:  (7.2)
(7.2)
и называется линейным однородным уравнением, в противном случае  оно называется линейным неоднородным уравнением.
оно называется линейным неоднородным уравнением.
Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:

 (7.3)
(7.3)
Выражение (7.3) есть общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция P(x) обозначает ту же функцию, что и в уравнении (7.2), применим прием, называемый методом вариации произвольной постоянной и состоящий в следующем: постараемся подобрать функцию С=С(x) так, чтобы общее решение линейного однородного уравнения (7.2) являлось бы решением неоднородного линейного уравнения (7.1). Тогда для производной функции (7.3) получим:
 .
.
Подставляя найденную производную в уравнение (7.1), будем иметь:

или  .
.
Откуда  , где
, где 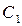 - произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет
- произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет  (7.4)
(7.4) 
Первое слагаемое в этой формуле представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое формулы (7.4) есть частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при  . Этот важный вывод выделим в виде теоремы.
. Этот важный вывод выделим в виде теоремы.
Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения  , то все остальные решения имеют вид
, то все остальные решения имеют вид  , где
, где  - общее решение соответствующего линейного однородного дифференциального уравнения.
- общее решение соответствующего линейного однородного дифференциального уравнения.
Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде 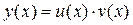 . Тогда
. Тогда  . Подставим найденную производную в исходное уравнение:
. Подставим найденную производную в исходное уравнение: 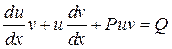 .
.
Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию u(x) за скобку: 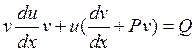 (7.5)
(7.5)
Потребуем обращения в нуль круглой скобки:  .
.
Решим это уравнение, полагая произвольную постоянную C равной нулю: 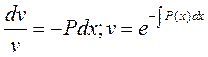 . С найденной функцией v(x) вернемся в уравнение (7.5):
. С найденной функцией v(x) вернемся в уравнение (7.5):  .
.
Решая его, получим:  .
.
Следовательно, общее решение уравнения (7.1) имеет вид:
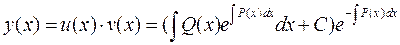 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Обобщенное однородное уравнение | | | Определение. Дифференциальное уравнение вида , где , называется уравнением Бернулли |
Дата добавления: 2015-07-26; просмотров: 225; Нарушение авторских прав

Мы поможем в написании ваших работ!