Основные равносильности булевых формул

Для любых формул A, B, C справедливы следующие равносильности:

1. Коммутативность.

а) A&B º B&A (для конъюнкции);

б) AVB º BVA (для дизъюнкции).

2. Ассоциативность.

а) A&(B&C) º (A&В)&C (для конъюнкции);

б) AV(BVC) º (AVB)VC (для дизъюнкции).

3. Дистрибутивность.

а) A&(BVC) º (A&B)V(A&C) (для конъюнкции относительно дизъюнкции);

б) AV(B&C) º (AVB)&(AVC) (для дизъюнкции относительно конъюнкции).

4. Закон де Моргана.

а) Ø(A&B) ºØAVØB (отрицание конъюнкции есть дизъюнкция отрицаний);

б) Ø(AVB) º ØA&ØB (отрицание дизъюнкции есть конъюнкция отрицаний).

5. Идемпотентность.

а) A&A º A (для конъюнкции);

б) AVA º A (для дизъюнкции).

6. Поглощение.

а) A&(AVB) º A (1–й закон поглощения);

б) AVA&B º A (2–й закон поглощения).

7. Расщепление (склеивание).

а) A&B V A&(ØB) º A (1–й закон расщепления);

б) (AVB) & (AVØB) º A (2–й закон расщепления).

8. Двойное отрицание.

Ø(ØA) º A.

9. Свойства констант.

а) A&1 º A; б) A&0 º 0; в) AV1 º 1; г) AV0 º A; д) Ø0 º 1; е) Ø1 º 0.

10. Закон противоречия.

A&ØA º 0.

11. Закон “исключенного третьего”.

AVØA º 1.

Правило равносильных преобразований

Пусть для формул A и B справедливо утверждение A º B. Пусть C_A – формула, содержащая A в качестве своей подформулы. Пусть C_B получается из C_A заменой A на B. Тогда C_A º C_B.

Принцип двойственности

Символы &, V называются двойственными.

Формула А^* называется двойственной формуле A, если она получена из A одновременной заменой всех символов &, V на двойственные.

Например,

A = xV(y&Øz);

A^* = x & (yVØz).

Теорема 3.1 (Принцип двойственности).

Если A º B, то A^* º B^*.

Определение 3.5. Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций (в вырожденном случае это может быть одна конъюнкция).

Пример: x, x&y, x V Øx&(Øy), Øx₁&x₂&(Øx₃) V x₁&(Øx₂)&x₃ V x₁&x₂&(Øx₃) – ДНФ.

(xVy)&Øx – не ДНФ.

Определение 3.6. Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, каждый конъюнктивный член которой содержит все переменные, либо их отрицания.

Пример 3.8

x&y, x&Øy V Øx&y – СДНФ функции двух переменных.

xVØx&y, xVy – не СДНФ.

Определение 2.9. Совершенной конъюнктивной нормальной формой (СКНФ) называется такая конъюнктивная нормальная форма, каждый дизъюнктивный член которой содержит все переменные, либо их отрицания.

Пример: xVy, (xVØy) &(ØxVy) – СКНФ функции двух переменных.

x &(ØxVy), x&y – не СКНФ.

Определение 3.8. Конъюнктивной нормальной формой (КНФ) называется формула, имеющая вид конъюнкции элементарных дизъюнкций (в вырожденном случае это может быть одна дизъюнкция).

Алгоритм 3.1. (Алгоритм приведения формул булевых функций к ДНФ (КНФ)).

Шаг 1. Все подформулы A вида B É C (т.е. содержащие импликацию) заменяем на ØBVC или на Ø(B&ØC).

Шаг 2. Все подформулы A вида B ~ C (т.е. содержащие эквивалентность) заменяем на (A&B) V (ØA&ØB) или на (AVØB)&(ØAVB).

Шаг 3. Все отрицания, стоящие над сложными подформулами, опускаем по законам де Моргана.

Шаг 4. Устраняем все двойные отрицания над формулами (в соответствии с равносильностью 8).

Шаг 5. Осуществляем раскрытие всех скобок по закону дистрибутивности конъюнкции относительно дизъюнкции для ДНФ (в соответствии с равносильностями 3а и 17) или по закону дистрибутивности дизъюнкции относительно конъюнкции для КНФ.

Алгоритм 3.2. (Алгоритм приведения формулы булевой функции к СДНФ)

Шаг 1. Используя алгоритм построения ДНФ, находим формулу В, являющуюся ДНФ формулы А.

Шаг 2. Вычеркиваем в B все элементарные конъюнкции, в которые одновременно входят какая-нибудь переменная и ее отрицание. Это обосновывается равносильностями:

A&ØA º 0, B&0 º 0, СV0 º С.

Шаг 3. Если в элементарной конъюнкции формулы B некоторая переменная или ее отрицание встречается несколько раз, то оставляем только одно ее вхождение. Это обосновывается законом идемпотентности для конъюнкции: A&A º A.

Шаг 4. Если в элементарную конъюнкцию С формулы В не входит ни переменная x, ни ее отрицание Øx, то на основании 1- го закона расщепления заменяем С на (С&x) V (C&Øx).

Шаг 5. В каждой элементарной конъюнкции формулы B переставляем конъюнктивные члены так, чтобы для каждого i (i = 1, ..., n) на i-м месте была либо переменная x_i, либо ее отрицание Øx_i.

Шаг 6. Устраняем возможные повторения конъюнктивных членов согласно закону идемпотентности для дизъюнкции: СVС º С.

Определение 3.10. ДНФ называется минимальной, если она содержит наименьшее общее число вхождений переменных среди всех равносильных ей ДНФ.

Определение 3.11. Импликантом булевой функции f(x₁, x₂, ... , x_n) называется элементарная конъюнкция С, не равная тождественно 0, такая, что C V f f. Отметим, что любая конъюнкция любой ДНФ в силу закона идемпотентности (равносильность 5б) является импликантом этой функции.

Алгоритм 3.5 (Алгоритм Квайна построения сокращенной ДНФ).

Шаг 1. Находим для данной булевой функции f ее формулу F, находящуюся в СДНФ.

Шаг 2. Находим все простые импликанты функции f. Для этого все элементарные конъюнкции формулы F попарно сравниваем между собой. Если две элементарные конъюнкции таковы, что они имеют вид C&x_i и C&Øx_i, то выписываем конъюнкцию С. Это является следствием 1-го закона расщепления (склеивания) (равносильность 7а). Конъюнкция С содержит n - 1 вхождение переменных. Элементарные конъюнкции, для которых произошло склеивание, помечаем. После построения всех конъюнкций, включающих n - 1 вхождение переменных, вновь сравниваем их попарно, производим, если возможно, склеивание, выписываем полученные конъюнкции из n - 2 членов, помечаем склеивающиеся конъюнкции из n - 1 членов и т.д. Процесс заканчивается, когда дальнейшее склеивание невозможно. Все непомеченные элементарные конъюнкции являются простыми импликантами. Их дизъюнкция даст нам формулу F₁, равносильную F, находящуюся в ДНФ и состоящую из простых импликантов, т.е. сокращенную ДНФ.

Упражнения для выполнения:

1.Записать СДНФ функции, заданной следующей картой Вейча:

2. Записать СДНФ функции, заданной следующей картой Вейча: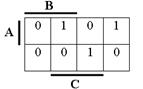

3. Записать минтерм, отмеченный на карте Вейча: .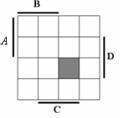

4. Найти сокращённую форму функции f = (0,3,4,7,8,10,11,12,15)

5. Найти сокращённую форму функции f = (1,3,5,12,15).

Контрольные задания для СРС

1. Минимизировать функции, заданные следующими таблицами:

А 1

		B

1
			D

2. Сколько клеток имеет карта Вейча n аргументов?

3. Укажите правильное определение понятия импликанты.

4. Укажите правильно определение понятия минтерма.

5. Построить таблицу истинности для выражения

(A & B Ú C) Þ (A Ú B Ú C).

6. Доказать 1-й закон де Моргана, не используя таблицу истинности.

Дата добавления: 2015-07-26; просмотров: 452; Нарушение авторских прав

Мы поможем в написании ваших работ!