Числа графов. Поиск маршрутов в графе. Цепи и циклы

Цель работы: Ознакомиться с основными понятиями части графов, с связностью, компонентами связности с числами графов. Научиться определять поиск маршрутов в графе.

Порядок выполнения работы:

Практическая работа рассчитана на 2 часа аудиторных занятий, включающих в себя следующее:

1. Изучить:

- Части графов. Связность, компоненты связности. Числа графов: цикломатическое, хроматическое, внешней и внутренней устойчивости.

- Поиск маршрутов в графе. Задача о минимальном соединении. Задача о кратчайшем пути.

- Эйлеровы цепи и циклы. Гамильтоновы цепи и циклы.

2. Решить упражнения к данному разделу. Выполнить каждый пункт упражнения согласно варианту. Вариант определяется как сумма двух последних цифр зачётной книжки, если количество заданий в пункте упражнения меньше, чем полученная цифра, то эта цифра делится пополам (берётся её целая часть).

3. Оформить отчет о проделанной работе в соответствии с требованиями.

4. Проработать контрольные задания СРС.

Требования к отчету:

Отчет по практической работе распечатывается в виде твердой копии и состоит из следующих пунктов:

Вариант индивидуального задания;

Результаты полученных решений заданий;

Ответы на контрольные задания СРС.

Методические указания

Пусть G - неориентированный граф. Маршрутомили цепью в G называется такая последовательность (конечная или бесконечная) ребер a₁, a₂,... a_n..., что каждые соседние два ребра a_i и a_i+1имеют общую инцидентную верши­ну. Одно и то же ребро может встречаться в маршруте несколько раз. В конечном маршруте (a₁,a₂,...a_n) имеется первое ребро a₁и последнее ребро a_n. Вершина x₁, инцидентная ребру a₁, но не инцидентная ребру a₂, называется началом маршрута, а вершина x_n, инцидентная ребру a_n, но не инцидентная ребру a_n-1, называется концом маршрута.

Длиной(или мощностью) маршрута называется число ребер, входящих в маршрут, причем каждое ребро считается столько раз, сколько оно вхо­дит в данный маршрут.

Замкнутый маршрут называется циклом.

Маршрут (цикл), в которой все ребра различны, называется простой цепью (циклом). Маршрут (цикл), в которой все вершины, (кроме первой и последней), различны, называется элементарной цепью (циклом).

Понятия пути, контура в ориентированном графе аналогичны понятиям маршрута, цикла в неориентированном графе.

Путем ориентированного графа называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей дуги.

Число дуг пути называетсядлиной пути.

Путь называется контуром, если его начальная вершина совпадает с конечной вершиной.

Путь (контур), в котором все дуги различны, называетсяпростым.

Путь (контур), в котором все вершины, кроме первой и последней, различны, называетсяэлементарным.

Следует усвоить, что понятиям ребра, маршрута, цепи, цикла в неориентированном графе соответствуют понятия дуги, пути, ориентированной цепи, контура в ориентированном графе. Для лучшего запоминания приведем эти термины в таблице.

Неориентированный граф называется связным, если каждая пара различных вершин может быть соединена по крайней мере одной цепью.

Ориентированный граф называется сильно связным, если для любых двух его вершин x_i и x_j существует хотя бы один путь, соединяющий x_i с x_j.

Ориентированный граф называется односторонне связным, если для любых двух его вершин по крайней мере одна достижима из другой.

Компонентой связности неориентированного графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа (максимально связный подграф).

Компонентой сильной связности ориентированного графа называется его сильно связный подграф, не являющийся собственным подграфом никакого другого сильно связного подграфа данного графа (максимально сильно связный подграф).

Компонентой одностронней связности неориентированного графа называется его односторонне связный подграф, не являющийся собственным подграфом никакого другого односторонне связного подграфа данного графа (максимально односторонне связный подграф).

Пусть G = (X, A) неориентирован­ный граф с множеством вершин X = {x₁,...,x_n}. Квадратная матрица S = (s_ij)порядка n, у которой

s_ij =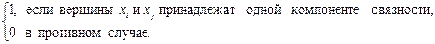

называется матрицей связности графа G.

Для ориентированного графа квадратная матрица T = (t_ij) порядка n, у кото­рой

t_ij =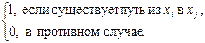

называетсяматрицей односторонней связности (достижимости).

Квадратная матрица S = (s_ij) порядка n, у которой

s_ij =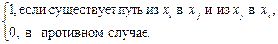

называется матрицей сильной связности.

Ориентированный граф называется нагруженным,если дугам этого графа поставлены в соответствие веса, так что дуге (x_i,x_j)сопоставле­но некоторое число c(x_i,x_j)= c_ij, называемое длиной(или весом,или стоимостьюдуги). Длиной(или весом или стоимостью) пути s, состоящего из некоторой последовательности дуг (x_i,x_j), называется число l(s), равное сумме длин дуг, входящих в этот путь, т.е.

l(s)= 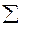c_ij, причем суммирование ведется по всем дугам(x_i, x_j) 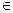s.

Матрица C = (c_ij) называется матрицей длин дуг или матрицей весов.

Для ненагруженного графа введем понятие кратчайшего пути. Это путь с минимальным общим числом дуг, причем каждая дуга считается столько раз, сколько она содержится в этом пути.

Для нахождения минимального пути между двумя произвольными верши­нами для случая, когда все c_ij ³0 можно воспользоваться простым алгоритмом Дейкстры. В общем случае задача решается с помощью ал­горитмов Флойда, Форда, Беллмана и др.

Алгоритмы нахождения минимального пути могут быть использованы для поиска кратчайших путей в ориентированном графе без контуров. Для этого нужно каждой дуге приписать вес, равный единице.

Рассмотрим следующую задачу:

В ориентированной, неориентированной или смешанной сети V найти кратчайший путь из заданной вершины i во все остальные вершины.

Решение (Дейкстpа, 1959 г.). Алгоритм использует три массива из N (= числу вершин сети) чисел каждый. Первый массив A содержит метки с двумя значения: 0 (вершина еще не рассмотрена) и 1 (вершина уже рассмотрена); второй массив B содержит расстояния - текущие кратчайшие расстояния от до соответствующей вершины; третий массив с содержит номера вершин - k-й элемент С[k] есть номер предпоследней вершины на текущем кратчайшем пути из Vi в Vk. Матрица расстояний D[i,k] задает длины дуге D[i,k]; если такой дуги нет, то D[i,k] присваивается большое число, равное "машинной бесконечности".

Алгоритм Дейкстры

1. (инициализация) В цикле от 1 до N заполнить нулями массив A; заполнить числом i массив C; перенести i-ю строку матрицы D в массив B, A[i]:=1; C[i]:=0 (i - номер стартовой вершины)

2. (общий шаг) Hайти минимум среди неотмеченных (т. е. тех k, для которых A[k]=0); пусть минимум достигается на индексе j, т. е. B[j]<=B[k].

Затем выполняются следующие операции:

A[j]:=1;

если B[k]>B[j]+D[j,k], то B[k]:=B[j]+D[j,k]; C[k]:=j

Условие означает, что путь Vi ... Vk длиннее, чем путь Vi...Vj Vk.

Если все A[k] отмечены, то длина пути от Vi до Vk равна B[k]. Теперь надо перечислить вершины, входящие в кратчайший путь).

3. (выдача ответа) Путь от Vi до Vk выдается в обратном порядке следующей процедурой:

3.1. z:=C[k];

3.2. Выдать z;

3.3. z:=C[z]. Если z =0, то конец, иначе перейти к 3.2.

Для выполнения алгоритма нужно N раз просмотреть массив B из N элементов, т. е. алгоритм Дейкстры имеет квадратичную сложность: O(n2).

 

Упражнения для выполнения:

1. Задача. Дан граф G = (X, U) рис1. Требуется построить цикл (цепь), проходящий через все ребра графа G ровно по одному разу. Иначе, заданную плоскую фигуру нарисовать , не отрывая каркндаша от бумаги и не проходя по одной и той же линии дважды.

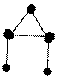рис.1

 

2. Задача. Для данного неорграф G рис 2. Определить цикломатическое число. Выяснить можно ли нарисовать G, не отрывая руки от бумаги и не проходя ни по одному ребру дважды.

 

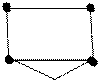Рис. 2

Контрольные задания для СРС

1. Как называется путь в графе, проходящий через каждую его вершину один раз?

2. Чему равен кратчайший путь в графе, содержащем цикл с отрицательным суммарным весом?

3. Укажите критерий, по которому можно проверить, что граф G имеет гамильтонов цикл.

4. Как называется последовательность ребер, в которой каждые два соседних ребра имеют общую вершину?

5. Как называется маршрут в неориентированном графе, в котором все ребра разные?

Рекомендуемая литература

1. Шевелев Ю. П. Дискретная математика. Ч. 2: Теория конечных автоматов. Комбинаторика. Теория графов (для автоматизированной технологии обучения): Учебное пособие. – Томск: Томск. гос. ун-т систем управления и радиоэлектроники, 1999

2. Дж. Андерсон Дискретная математика и комбинаторика: Пер. с англ. – М.: Вильямс, 2003. 960 с.

3. Новиков Ф. А. Дискретная математика для программистов СПб.: Питер, 2004. 302 с.

4. Н. Кристофидес. Теория графов Алгоритмический подход М.: Мир, 1978

Рассмотрено на заседании Одобрено учебно-методическим бюро ИКТС

кафедры _ВТиПО________ Протокол № _______

"____" ____________ 20____ г. Председатель учебно-методического бюро

Протокол № ______________ ИКТС

Зав. кафедрой ___ ВТиПО ______________ Капжаппарова Д.У.

__________ Когай Г.Д. "____" ____________ 20 ____ г.

Дата добавления: 2015-07-26; просмотров: 585; Нарушение авторских прав

Мы поможем в написании ваших работ!