Транспортная задача. В простейшем варианте эта задача возникает, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям

В простейшем варианте эта задача возникает, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям. Предполагается, что потребителям безразлично откуда (из каких пунктов производства будет поступать продукт), лишь бы он поступал в запрашиваемом объеме. Однако от того, насколько рациональным будет прикрепление пунктов потребления к пунктам производства, существенно зависит объем работы транспорта. В этой связи возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок груза, при котором потребности удовлетворяются, а затраты на транспортировку минимальны.

Математическая модель задачи описывается так.

Пусть имеется m пунктов производства в единицу времени (месяц, квартал), равными a_i=( 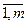) и n пунктов потребления с объемами потребления b_i I( ). Естественно полагать, что a_i 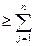b_j, т.е. потребление не превышает возможностей производства. Известны также величины c_ij—затраты по перевозке единицы продукта из I-го пункта производства в j-й пункт потребления.

Необходимо составить такой план перевозок, при котором были бы удовлетворены потребности во всех пунктах потребления и при этом суммарные затраты на перевозку были бы минимальными.

Обозначая через x_ij количество продукта, перевозимое из I –го пункта производства в j-й пункт потребления, приходим к следующей математической модели:

Найти значения величин x_ij, чтобы достигался

min c_ij x_ij суммарных затрат на транспортировку при условиях:

1. 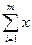_ij 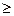b_j, j= —в каждый пункт потребления завозится требуемое количество продукта.

2. x_ij a_i, I= 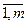— из каждого пункта производства вывозится не более произведенного количества продукта.

1. x_ij= 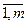, — перевозимый объем продукта , не может быть отрицательным.

Эта задача может быть поставлена и в параметрической постановке, например, зависеть от времени.

Дата добавления: 2015-07-26; просмотров: 167; Нарушение авторских прав

Мы поможем в написании ваших работ!