
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тема 1. Задачи теории автоматов. Понятие абстрактного автомата. Конечные автоматы. Основные модели автоматов
ЭЛЕМЕНТЫ Теории автоматов
(теоретическая часть раздела)
Модуль 1.
План.Основные определения. Решаемые задачи. Виды автоматов. Модели Мура и Мили. Способы описания и задания конечных автоматов. Переход от одной модели автомата к другой.
Тема 1. Задачи теории автоматов. Понятие абстрактного автомата. Конечные автоматы. Основные модели автоматов.
Теория автоматов – раздел теории управляющих систем (теоретической кибернетики), изучающий математические модели преобразователей дискретной информации. Теория возникла в середине ХХ века в связи с бурным развитием аппаратных средств электронной вычислительной техники, решением практических вопросов проектирования цифровых ЭВМ, а также изучением так называемых «нейронных сетей», в качестве математических моделей которых рассматривались конечные автоматы. Теория автоматов тесно связана с теорией алгоритмов и более всего с таким ее разделом, как теория абстрактных машин. Автоматы можно считать частным случаем последних. Само слово «автомат» греческого происхождения: ’αυτομάτος буквально означает «самодействующий».
В теории автоматов решаются следующие основные задачи: анализ и синтез автоматов, определение полноты, минимизация и эквивалентные преобразования автоматов. Кратко сформулируем постановку каждой из перечисленных задач.
Задача анализа: по заданному автомату описать его поведение. Или: по неполному описанию автомата установить некоторые его свойства.
Задача синтеза: построить автомат с наперед заданным поведением (алгоритмом функционирования). Задачу синтеза принято рассматривать двояко: абстрактный синтез как построение математической модели автомата и структурный синтез как разработку функционально-логической схемы автомата.
 Задача полноты: определить, обладает ли совокупность автоматов, составляющих множество M’ M, свойством полноты. Иными словами, если ко всем автоматам множества M’конечное число раз применить операцию суперпозиции, то совпадут ли M’и M?
Задача полноты: определить, обладает ли совокупность автоматов, составляющих множество M’ M, свойством полноты. Иными словами, если ко всем автоматам множества M’конечное число раз применить операцию суперпозиции, то совпадут ли M’и M?
Задача минимизации: построить автомат, минимальный заданному. Минимальный автомат обладает наименьшей мощностью |S| при функциональной эквивалентности заданному автомату. Задача решается путем определения классов эквивалентности состояний автомата.
Задача эквивалентных преобразований: определить систему правил преобразования автомата (так называемую «полную систему правил»), которая позволила бы преобразовывать произвольный автомат в любой ему эквивалентный. В частности, задачей эквивалентных преобразований является задача перехода от одной модели автомата к другой.
Заметим: два автомата (функционально) эквивалентны, если их поведение одинаково при воздействии одних и тех же последовательностей входных сигналов. В таком случае говорят о совпадении моделей поведения двух автоматов.
Основными понятиями теории автоматов являются следующие:
— понятие абстрактного автомата (АА);
— понятие композиции автоматов.
Понятие АА позволяет рассматривать дискретные устройства с точки зрения алгоритмов их функционирования, т.е. реализуемых ими алгоритмов преобразования дискретной информации.
Абстрактным автоматом называют модель, описываемую пятиместным кортежем:
А = (X, Y, S, fy, fs),
где первые три компонента – непустые множества:
X – множество входных сигналов АА,
Y – множество выходных сигналов АА,
S – множество состояний АА,
а два последних компонента кортежа – характеристические функции:
fy – функция выходов;
fs – функция переходов АА из одного состояния в другое.
Если множества X, Y, S – конечные, то такой АА называют конечным автоматом (КА). Как правило, множества задают перечислением их элементов и вводят обозначения мощностей:
X = {x1, x2, …, xp}, |X| = p;
Y = {y1, y2, …, yq}, |Y| = q;
S = {s1, s2, …, sn}, |S| = n.
КА, в описание которого входят определенные таким образом множества, называют иногда (n, p, q)-автоматом. Сами множества нередко называют векторами, например: вектор входных сигналов, вектор состояний.
Если хотя бы одно из перечисленных множеств является бесконечным, то такой АА называют бесконечным. Дальнейшее изложение будем вести, исходя из практических соображений, применительно к конечным автоматам.
Все автоматы, в том числе конечные, функционируют в дискретном исчислении времени. Моменты времени образуют ряд целых неотрицательных чисел: 0, 1, 2, 3, …
В каждый дискретный момент времени КА находится в одном и только одном состоянии Si, воспринимает одно значение вектора X и выдает на выходе одно значение вектора Y. Принято считать, что в начальный момент времени t = 0 автомат находится в начальном состоянии S0, которое можно включить отдельным, шестым, компонентом кортежа:
А = (X, Y, S, fy, fs, S0).
Автомат с выделенным начальным состоянием называют инициальным.
Общую схему автомата можно представить в виде некоторого «черного ящика», осуществляющего преобразование вектора входных сигналов в вектор выходных сигналов (рис. 1.1):
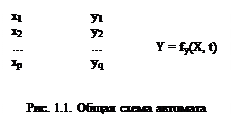


Для учета фактора времени в приведенном уравнении для yi служит вектор состояний S, как своего рода «память о прошлом». Действительно, на одно и то же значение вектора X автомат будет выдавать разные значения выходных сигналов в зависимости от состояния, в котором он оказался в данный момент времени согласно алгоритму функционирования.
Рассмотрим характеристические функции автомата.
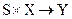
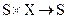 Функция fs реализует бинарное отношение вида , т.е. каждой паре «состояние – входной сигнал» ставит в однозначное соответствие определенное состояние из множества S. Аналогично, функция fy задает отношение , т.е. каждой паре «состояние – входной сигнал» ставит в соответствие конкретный выходной сигнал – элемент множества Y.
Функция fs реализует бинарное отношение вида , т.е. каждой паре «состояние – входной сигнал» ставит в однозначное соответствие определенное состояние из множества S. Аналогично, функция fy задает отношение , т.е. каждой паре «состояние – входной сигнал» ставит в соответствие конкретный выходной сигнал – элемент множества Y.
Характеристические функции определяют, соответственно, в какое состояние sÎS перейдет автомат в следующий, (t+1)-й момент времени и каково будет значение выходного сигнала yÎY в текущий момент времени t:
| s(t+1) = fs(x(t), s(t)) | (1) |
| y(t) = fy(x(t), s(t)) |
Из приведенных уравнений видно, что аргументами характеристических функций являются текущее значение входного сигнала и текущее состояние.
КА, заданный парой уравнений (1), называется автоматом I рода, или автоматом Мúли (Mealy). На практике часто встречаются автоматы, выходные сигналы которых в момент времени t однозначно определяются текущим состоянием автомата и не зависят от вектора входных сигналов:
| s’(t+1) = fs’(x(t+1), s’(t)) | (2) |
| y(t) = fy’(s’(t)) |
Автомат, заданный парой уравнений (2), называют автоматом II рода, или автоматом Мура (Moore). Штрих введен в обозначения для отличия функций и состояний автомата Мура от автомата Мили. Заметим, что автомат Мили по отношению к автомату Мура «запаздывает» на один дискретный момент времени по входному сигналу.
Автоматы I и II рода являются двумя основными моделями, изучаемыми теорией автоматов.
Если для выходного сигнала некоторого КА имеет место уравнение: y(t) = fy(x(t)), то такой автомат называется тривиальным. Строго говоря, это уже не автомат, а комбинационная схема (КС), реализующая булеву функцию fy для выходного сигнала y (рис. 1.2.).

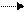

На практике автомат представляет собой совокупность двух автоматов – операционного и управляющего. Операционный автомат выполняет ряд действий над входными данными и выдает результат, а управляющий автомат задает последовательность этих действий, т.е. алгоритм функционирования операционного автомата. Например, в случае кодового замка операционным автоматом является электромагнит, управляющий засовом, а управляющий автомат – это схема, обеспечивающая считывание и анализ сигналов от клавиш, проверку кода, выдачу сигнала операционному автомату на открытие замка, сброс в начальное состояние.
Или другой пример – устройство умножения двоичных чисел с фиксированной запятой. Операционный автомат представляет собой ряд взаимосвязанных функциональных элементов – сумматор (например, дополнительного кода), регистры входных данных и результата, сдвиговый регистр, цепи переноса двоичной единицы. Управляющий автомат задает порядок, в котором должны действовать элементы операционного автомата, чтобы обеспечить последовательность шагов реализуемого алгоритма умножения.
| <== предыдущая страница | | | следующая страница ==> |
| Генерация команд сравнения и перехода | | | Тема 2. Абстрактный синтез конечного автомата |
Дата добавления: 2015-07-26; просмотров: 555; Нарушение авторских прав

Мы поможем в написании ваших работ!