Тема 3. Рекурсивные функции

План лекции

1. Рекурсивная функция

2. Понятие простейших функций

Примитивно-рекурсивные и частично-рекурсивные функции

Типы рекурсивных алгоритмов

Числовые функции, значение которых можно установить посредством некоторого алгоритма, называются вычислимыми функциями.

Для того чтобы описать класс функций с помощью рекурсивных определений, рассмотрим набор простейших функций:

1) Z(x₁, x₂, ..., x_n) = 0 - нуль-функция, которая определена для всех неотрицательных значений аргумента;

2) s(x) = x+1 - функция непосредственного следования, также определенная для всех целых неотрицательных значений своего аргумента;

3) 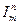(x₁, x₂, . . ., x_m, . . . , x_n) = x_m - функция выбора (тождества), повторяющая значения своих аргументов.

Используя простейшие функции в качестве исходных функций, можно с помощью небольшого числа общих конструктивных приемов строить сложные арифметические функции. В теории рекурсивных функций особо важное значение имеют три операции: суперпозиции, примитивной рекурсии и минимизации.

Оператор суперпозиции

Оператором суперпозиции S называется подстановка в функцию от m переменных m функций от n одних и тех же переменных. Она дает новую функцию от n переменных. Например, из функций f(x₁, x₂, ..., x_m), f₁(x₁, x₂, ..., x_n), f₂(x₁, x₂, ..., x_n), . . ., f_m(x₁, x₂, ..., x_n) можно получить новую функцию:

S^m+1(f, f₁, f₂, ..., f_m) = g(x₁, x₂, ..., x_n) = f(f₁(x₁, x₂, ..., x_n), f₂(x₁, x₂, ..., x_n), ..., f_m(x₁, ..., x_n)). (1)

В операции суперпозиции S^m+1 индекс сверху указывает на число функций.

Таким образом, при помощи оператора суперпозиции и функции выбора можно выразить любую подстановку функции в функцию. Например, осуществляя операцию суперпозиции функций f(x) = 0 и g(x) = x+1, получим функцию:

h(x) = g(f(x)) = 0 + 1 = 1.

При суперпозиции функции g(x) с этой же функцией получим функцию h(x) = g(g(x)) = x + 2.

Используя подстановку и функции тождества, можно переставлять и отождествлять аргументы в функции:

f(x₂, x₁, x₃, . . ., x_n) = f(I₂²(x₁, x₂), I₁²(x₁, x₂), x₃, . . ., x_n);

f(x₁, x₁, x₃, . . ., x_n) = f(I₁²(x₁, x₂), I₁²(x₁, x₂), x₃, . . ., x_n).

Таким образом, если заданы функции тождества и операторы суперпозиции, то можно считать заданными всевозможные операторы подстановки функций в функции, а также переименования, перестановки и отождествления переменных.

Оператор примитивной рекурсии

Оператор примитивной рекурсии R_n позволяет определить (n+1) - местную функцию f по двум заданным функциям, одна из которых является n- местной функцией g, а другая (n+2) - местной функцией h.

Функция f(x₁, x₂, ..., x_n, y) получается оператором примитивной рекурсии из функций g(x₁, x₂, ..., x_n) и функции h(x₁, x₂, ..., x_n, y, z), если:

f(x₁, x₂, ..., x_n, 0) = g(x₁, x₂, ..., x_n); (2)

f(x₁, x₂, ..., x_n, y+1) = h(x₁, x₂, ..., x_n, y, f(x₁, x₂, ..., x_n, y)).

Приведенная пара равенств (2) называется схемой примитивной рекурсии. Для понимания операции примитивной рекурсии необходимо заметить, что всякую функцию от меньшего числа аргументов можно рассматривать как функцию от большего числа аргументов. Существенным в операторе примитивной рекурсии является то, что независимо от числа переменных в f рекурсия ведется только по одной переменной у. Остальные n переменных x₁, x₂, ..., x_n на момент применения схемы (2) зафиксированы и играют роль параметров.

Оператор минимизации

Отношение P(x₁, x₂, ..., x_n) называется примитивно-рекурсивным, если примитивно- рекурсивна его характеристическая функция:

.

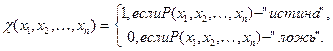Предикат называется примитивно-рекурсивным, если его характеристическая функция примитивно-рекурсивна.

Функция f(x₁, x₂, ..., x_n) получается посредством оператора минимизации из предиката P(x₁, x₂, ..., x_n, z), если в любой точке значением функции f(x₁, x₂, ..., x_n) является минимальное значение z, обращающее предикат P(x₁, x₂, ..., x_n, z) в значение «истина»:

f(x₁, x₂, ..., x_n) = 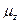(P(x₁, x₂, ..., x_n, z)),

где 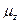– оператор минимизации.

Ограниченный оператор минимизации

Функция f(x₁, x₂, ..., x_n) получается ограниченным оператором минимизации из предиката P(x₁, x₂, ..., x_n, z) и функции U(x₁, x₂, ..., x_n), если в любой точке значение этой функции определено следующим образом:

1) для любого z < U(x₁, x₂, ..., x_n) такого, что P(x₁, x₂, ..., x_n, z) = "истина", значение функции f(x₁, x₂, ..., x_n) = 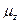(P(x₁, x₂, ..., x_n, z)),

2) не для любого z < U(x₁, x₂, ..., x_n) такого, что P(x₁, x₂, ..., x_n, z) = "истина", значение функции f(x₁, x₂, ..., x_n) = U(x₁, x₂, ..., x_n).

Данное определение записывается следующим образом:

f(x₁, x₂, ..., x_n) = 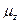< U(x) (P(x₁, x₂, ..., x_n, z)).

Ограничение z в ограниченном операторе минимизации дает гарантию окончания вычислений, поскольку оно оценивает сверху число вычислений предиката P. Возможность оценить сверху количество вычислений является существенной особенностью примитивно- рекурсивных функций.

Дата добавления: 2015-07-26; просмотров: 149; Нарушение авторских прав

Мы поможем в написании ваших работ!