Расчет коротких трубопроводов

Для вывода расчетной зависимости применим уравнение Бернулли, используя следующую схему.

1. Намечаем два сечения, в которых движение плавноизменяющееся и для которых будем записывать уравнение Бернулли.

Сечения следует выбирать так, чтобы как можно больше слагаемых, входящих в уравнение Бернулли, было в этих сечениях задано. Если кроме уравнения Бернулли не предполагается использовать какие-либо другие равенства, то следует так выбирать сечения, чтобы в уравнении Бернулли было неизвестно лишь одно слагаемое. Так, при решении задачи для трубопровода, представленного на рис. 6.2, считаем, что сечение 1 — 1 совпадает со свободной поверхностью: здесь известно, что давление P₁ равно атмосферному р_а, скорость жидкости Vj равна нулю (считаем, что резервуар достаточно большой и скоростным напором вследствие снижения уровня воды в нем и изменением отметки свободной поверхности по сравнению с суммарными потерями напора можно пренебречь). Далее задаем, что сечение 2—2 совпадает с выходным сечением трубопровода; здесь известно, что давление р₂ =р_а, а скорость v₂ равна выходной скорости.

При решении прямой задачи в варианте: a) задают отметку уровня свободной поверхности жидкости в резервуаре z₁ а неизвестной является v₂, в варианте б) задают v₂ (или расход Q) и определяют

отметку z₁.

Рис. 6.2. Истечение жидкости из резервуара через короткий трубопровод в атмосферу

2. Намечаем плоскость сравнения. Это произвольная горизонтальная плоскость; для упрощения решения задачи выбрать ее следует так, чтобы z₁ или z₂ обратились в ноль: например, плоскость 0—0 на рис. 6.2 проведена так, что z₂ = 0.

3. Записываем уравнение Бернулли

z₁ + p₁/pg + ₁v₁/2g = z₂ + p₂/pg + ₂v₂/2g + h_f (2.22)

Определяем значения слагаемых, входящих в (6.З).

В практических расчетах обычно полагают = 1,0. Представляем общие потери напора h_f в виде суммы

h_f = h_l1 +h_ll1' + h_l11”; +h_ВХ+h_pp +h_f, (2.23)

где 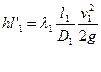, - потери напора по длине; v, и v₁₁ –средние скорости на I и II участках трубопровода, соответственно, v₁₁ = v₂, а из уравнения неразрывности 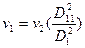; 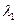, 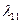- коэффициенты гидравлического трения на первом и втором участках трубопровода;

~~ потери напора на вход в трубопровод;

-потеря на резкое расширение;

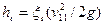— потеря на задвижке.

5. Подставляя полученные результаты в (2.22), получаем

(2.24)

Если решается прямая задача (т.е. заданы D₁, и D₁₁ ) и рассматривается вариант а),(задано значение Q), то легко найти на каждом участке v₁, v₂ и соответствующие числа Re_D = vD/v. Затем, используя справочные данные, определяем абсолютную шероховатость 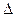и коэффициенты местных потерь напора 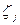и далее по относительной шероховатости 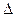_r = 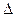/D и числу Рейнольдса Re_D находим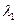 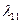. Для этого можно воспользоваться либо графиком Кольбрука—Уайта (см. рис. 5.21), либо какой-нибудь эмпирической зависимостью, аппроксимирующей этот график, — (5.114), (5.116) или (5.117). Значение Н вычисляется по зависимости (2.24).

Вариант б) прямой задачи (задано значение Н, а вычисляется Q), то зависимость (2.24) представляют в виде

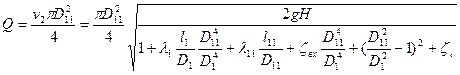(2.25)

или ,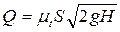

где — коэффициент расхода трубопровода, 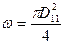— площадь выходного сечения.

Зависимость (6.5) представляет собой общую расчетную формулу для коротких трубопроводов с произвольным (не только круглым) поперечным сечением. В этой формуле коэффициент расхода

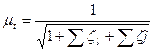, (2.26)

где 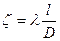— коэффициент потери подлине. Значения и 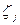следует включать в расчет, учитывая отличие площади поперечного сечения трубопровода на участке, к которому они относятся, от площади выходного сечения, как это сделано в формуле (2.25).

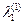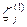Поскольку и Q, и v₁, и v₁₁ неизвестны, то нельзя определить значения Re_D, а следовательно, и . Задачу обычно решают методом последовательных приближений, причем в качестве первого приближения целесообразно принять, что и j соответствуют области квадратичного сопротивления и не зависят от Re_D. Тогда, определив по значению относительной шероховатости и , а также значения вычисляем в первом приближении Q⁽¹⁾. По этому значению Q⁽¹⁾ вычисляем Re_D и находим уточненные значения 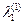и , , 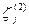используя которые вычисляем по формуле (2.25) расход во втором приближении Q⁽²⁾. Как показывает опыт расчетов, обычно Q⁽²⁾ отличается от Q⁽¹⁾ не более чем на 5 %, что считается достаточным, чтобы ограничиться вторым приближением и считать искомое значение Q = Q⁽²⁾. Если Q⁽²⁾ сильно (более чем на 5 %) отличается от Q⁽¹⁾, следует сделать третье приближение.

Обратную задачу, когда заданы Q и Н, а неизвестны значения D₁,и D₁₁ решают графически. Задавая несколько значений D₁ (при постоянном заданном условием задачи отношении D₁,и D₁₁) и принимая расход равным заданному, сводят задачу к первому варианту прямой задачи; строят зависимость Н = f (d₁ ) и по заданному значению Н определяют требуемое значение D1 (рис. 6.3), а затем по заданному отношению D₁/D₁₁ находят D₁. Здесь следует отметить, что полученные в результате расчета значения D₁ и D₁₁, как правило, должны быть округлены в большую или меньшую сторону и приняты в соответствии с сортаментом на трубы.

Расчет коротких труб обычно следует заканчивать построением пьезометрической и напорной линий. Для этого вычисляют значения h_вх,h_д1, h_{pp ,} h_l11, h 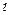, их, как показано на рис. 6.2, строят напорную линию Е—Е. Пьезометрическую линию Р—Р строят, откладывая от напорной линии вниз величину скоростного напора на данном участке трубы. Пьезометрическая линия проходит через центр тяжести выходного сечения 2—2, так как здесь избыточное давление равно нулю и z₂ +p₂/ 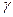= ^Z2

Дата добавления: 2015-07-26; просмотров: 252; Нарушение авторских прав

Мы поможем в написании ваших работ!