Теория двойственности

Рассмотрим пару задач ЛП вида:

(I) (II)

… …

… …

… …

… …

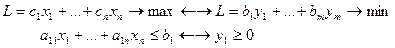
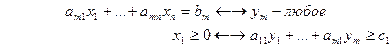
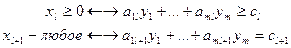
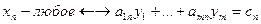
Задачу (I) называют прямой задачей ЛП, а (II) – двойственной. Неравенства задач (I) и (II), соответствующие друг другу (по стрелке), называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т.е. соотношение двойственности взаимное. Поэтому можно любую из такой пары задач считать прямой, а другую двойственной.

Для каждой задачи ЛП можно построить двойственную ей задачу по правилам:

1) в задаче максимизации все ограничения-неравенства привести к виду «меньше или равно», а в задаче минимизации - к виду «больше или равно»;

2) число переменных одной задачи равно числу ограничений другой задачи;

3) матрица коэффициентов ограничений одной задачи является транспо­нированной матрицей коэффициентов ограничений другой задачи;

4) вектор коэффициентов целевой функции одной задачи является вектором правых частей ограничений другой задачи;

5) ограничению-неравенству одной задачи соответствует неотрицательная переменная другой задачи; ограничению-равенству соответствует переменная, не имеющая ограничение на знак (и наоборот).

Двойственность является одним из фундаментальных понятий в теории ЛП. Исключительно важную роль играют следующие утверждения, получившие названия теорем двойственности.

Первая теорема двойственности. Если одна из пары двойственных задач (I) и (II) разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают:

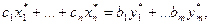
где 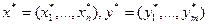– оптимальные планы задач (I) и (II) соответственно.

Говорят, что допустимые решения x,y удовлетворяют условиям дополняющей нежесткости (УДН), если при подстановке этих векторов в ограничения задач (I) и (II) хотя бы одно из любой пары сопряженных неравенств обращается в равенство.

Вторая теорема двойственности. 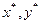оптимальны в задачах (I) и (II) тогда и только тогда, когда они удовлетворяют УДН.

Дата добавления: 2015-07-26; просмотров: 163; Нарушение авторских прав

Мы поможем в написании ваших работ!