
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Практический блок
Пример 1.Рассмотрим проблему математического моделирования на примере задачи оптимизации параметров реорганизационной политики.
Для большинства неплатежеспособных предприятий неудовлетворительная структура баланса отождествляется с отставанием фактического уровня текущей ликвидности от его норматива (Ктл<2) даже при достаточном уровне обеспеченности собственными средствами (Косс ³0,1).
Реорганизационные политики – процедуры реструктуризации балансов – позволяют перевести их в удовлетворительную структуру за счет реализации специально подобранного комплекса организационно-технических мероприятий. Но однозначно выбрать для практической реализации из возможных вариантов реорганизационных политик один, наиболее рациональный затруднительно, так как, если по прогнозируемым показателям платежеспособности, структуры баланса они равнозначны, то по прогнозным финансовым результатам могут быть противоречивыми.
Оценить предпочтительность каждого из этих вариантов оказывается возможным, если сформулировать задачу оптимизации реорганизационных политик с помощью математической модели, которая будет определяться текущим уровнем финансовой состоятельности, прежде всего, сложившимся уровнем платежеспособности.
Задача оптимизации основных параметров текущей деятельности может быть представлена следующей общей постановкой:
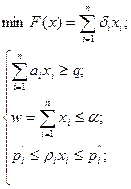
где F(x) – целевая функция задачи;
хi – независимые искомые переменные по направлениям реорганизационной политики (вектор управления структурой имущества: искомая величина продаж одного вида средств, приобретения другого, погашения долгов);
di – экспертная оценка приоритетности i-го направления реорганизации;
w – константа обеспечения текущей ликвидности (w=2КЗ – ОА; КЗ – краткосрочная задолженность, ОА – оборотные активы);
аi – коэффициенты при неизвестных переменных в ограничении на обеспеченность собственными оборотными средствами;
q – минимально-допустимый уровень обеспеченности собственными оборотными средствами (q = ВА + 0,1ОА – КР; ВА – внеоборотные активы, КР – капитал и резервы);
а – верхний предел допустимых продаж и приобретений активов;
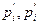 – соответственно нижняя и верхняя границы возможного изменения i-го вида активов;
– соответственно нижняя и верхняя границы возможного изменения i-го вида активов;
ri – удельный вес i-го вида активов предприятия в общей стоимости его имущества.
В частности, применительно к типичной неудовлетворительной структуре баланса Ктл < 2, Косс ³ 0,1, характерной для большинства неплатежеспособных предприятий, ищем такие х1 – объем продаж части активов, х2 – размер погашения кредиторской задолженности, чтобы выполнилось условие Ктл = 2 при сохранении Косс ³ 0,1. Тогда модель приобретает вид:
Ктл = (ОА + х1 – х2)/(КЗ – х2) = 2, откуда х1 + х2 = 2КЗ – ОА;
Косс = (КР – ВА + х1)/(ОА + х1 – х2) ³ 0,1, откуда
0,9 х1 + 0,1 х2 ³ ВА +0,1ОА – КР;
х2 – х1 £ a×ОА;
х1 £ b×ВА;
х2 £ g×КЗ,
где a, b, g – предельно допустимые для сохранения статуса деятельности предприятия размеры уменьшения соответственно оборотных активов (например, до 20%), внеоборотных активов (10%), краткосрочной задолженности (50%).
Целевая функция
min(d1х1 + d2х2),
где d1, d2 – экспертные оценки значимости продажи имущества и погашения наиболее срочных обязательств.
Приведенная выше задача может быть решена методами линейного программирования, которые будут рассмотрены в теме 2.2. Однако встречаются математические модели, которые решить аналитически невозможно. Для их решения существуют специальные методы численного решения. Особенностью таких методов является наличие погрешности в результатах. Погрешность в результатах определяется неточностью модели, т.е. ошибочностью или недостаточностью положений, лежащих в основе построенной модели, и погрешностью математических методов, с помощью которых проводился анализ изучаемой модели.
Представленные ниже в темах 2.2 – 2.9 модели и методы в основном ориентированны на те задачи, которые попадают в сферу исследования операций в управленческой и экономической деятельности и могут быть полностью или частично использованы при их математическом моделировании.
Пример 2. Из четырёх видов основных материалов (медь, цинк, свинец, никель) составляют три вида сплавов латуни: обычный, специальный и для художественных изделий. Цены единицы веса меди, цинка, свинца и никеля составляют 0,8 руб., 0,6 руб., 0,4 руб. и 1,0 руб., а цена единицы веса сплава, соответственно, 2 руб., 3 руб., 4 руб. Сплав для художественных изделий должен содержать не менее 6% никеля, не менее 50% меди и не более 30% свинца; специальный – не менее 4% никеля, не менее 70% меди, не менее 10% цинка и не более 20% свинца. В обычный сплав компоненты могут входить без ограничения. Производственная мощность предприятия позволяет выпускать (за определённый срок) не более 400 ед. веса обычного сплава, не более 700 ед. веса специального сплава и не более 100 ед. веса сплава для художественных изделий.
Построить математическую модель задачи нахождения производственного плана, обеспечивающего максимальную прибыль.
Решение. Обозначим через xij долю i-той компоненты (1-медь, 2- цинк, 3-свинец, 4-никель) в j-том виде сплава (1-обычный, 2-специальный и 3-для художественных изделий). уj – количество j-того вида сплава.
Тогда получим следующие ограничения модели:
x11 + x21 + x31 + x41 =1;
x12 + x22 + x32 + x42 =1; (2.1.1)
x13 + x23 + x33 + x43 =1.
Ограничения на состав компонент в смесях:
x12 ≥0.7; x22 ≥0.1; x32 ≤0,2; x42 ≥0,04;
x13 ≥0.5; x33 ≤0,3; x43 ≥0,06. (2.1.2)
Ограничесния на производственную мощность предприятия:
у1 ≤400; у2 ≤700; у3 ≤100;
Требование неотрицательности переменных:
у j ≥0, xij ≥0. i=1,…,4, j=1,2,3. (2.1.3)
Целевая функция представляет собой сумму прибыли:
((2-0.8)x11 + (2-0.6)x21 + (2-0.4)x31 +(2-1) x41) у1+
((3-0.8)x12 + (3-0.6)x22 + (3-0.4)x32 +(3-1)x42) у2+ (2.1.4)
((4-0.8)x13 + (4-0.6)x23 + (4-0.4)x33 + (4-1)x43) у3 →max
Ограничения (2.1.1-2.1.3) и целевая функция (2.1.4) представляют собой математическую модель для получения искомой информации.
Пример 3. (Размещение заказов). Фирма получила заказ на несколько тысяч новых изделий, собирающихся из отдельных блоков. Руководство фирмы приняло решение разместить заказы на изготовление n блоков и выбрало n фирм-поставщиков. Каждый заказ настолько велик, что фирма-поставщик не может выполнить более одного заказа. Каждому поставщику предложено определить стоимость выполнения заказа, т.е. цену, по которой он готов поставить фирме различные блоки. Фирма должна заключить n контрактов на поставку ей n видов блоков, минимизировав при этом свои общие затраты на приобретение комплектующих узлов со стороны.
Обозначим: i - номер (название) блока, i = 1,....n; j - номер (название) фирмы-поставщика, j= 1,...,n; сij - стоимость выполнения i-ro блока j-ой фирмой (заданное число). Кроме того, введем для каждого i и j число.
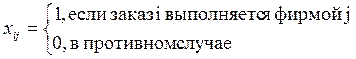
Целевая функция, имеющая смысл общих затрат на покупку комплектующих блоков, запишется так
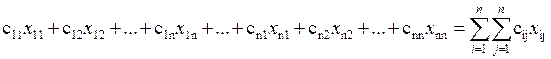 Ограничения задачи (на переменные хij) имеют следующий смысл:
Ограничения задачи (на переменные хij) имеют следующий смысл:
1) каждый i-й блок должен быть выполнен (каким-либо поставщиком);
2) каждая фирма-поставщик j должна выполнить один (какой-либо) блок .
Математически эти условия запишутся соответственно:
xi1+xi2 +…+ xin = 1, i = 1,....n;
x1j+x2j +…+ xnj = 1, j= 1,...,n.
Таким образом, приходим к следующей оптимизационнойзадаче (модели):
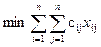
при ограничениях
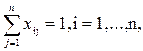
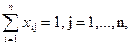
xij = 0 или 1 для всех i,j.
Пример 4. (Выбор портфеля ценных бумаг). Специалисту по финансовому анализу, работающему в банке (или в страховой компании) требуется определить наилучший набор акций, облигации и других ценных бумаг на выделенную сумму с целью минимизации риска, связанного с приобретением набора ценных бумаг.
Прибыль к концу планового периода на каждый доллар, вложенный в бумагу j-го вида, характеризуется двумя показателями: аj - фактическая прибыль (случайное число), aj - ожидаемая прибыль. Требуется, чтобы ожидаемая прибыль на доллар инвестиций была для всего набора ценных бумаг не ниже заданной величины b.
Для получения модели примем все средства, выделенные на покупку ценных бумаг, равными единице, и обозначим через xj - долю от всех средств, выделяемую для приобретения ценных бумаг вида j.
Риск учитывается при помощи ковариации (см. теорию вероятностей)
прибыли для ценных бумаг вида i и вида j:
sij = М (аi - ai) (аj - aj)
Математическая модель имеет вид:
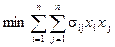
при ограничениях
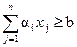
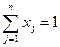
xj ³ 0, j=1,…,n
Здесь n - число разновидностей ценных бумаг. Целевая функция имеет смысл дисперсии фактической прибыли (отклоние фактической прибыли от ожидаемой), первое ограничение есть условие на ожидаемую прибыль, а последнее - непревышение средств, выделенных на покупку ценных бумаг.
Пример 5. (Задача о рекламе). Фирма планирует проведение радиорекламной кампании по сбыту автомобилей в одном из регионов, где расположено s радиостанций, в течение двух недель. Фирма оценила предварительно, что если радиостанции j выделить уj долларов, то чистый доход от увеличения сбыта равен Rj(yj) (Rj - функция реализации дохода от объема финансирования рекламы). На рекламу выделена общая сумма, равная N долларам. Число рекламных объявлений в день не должно превышать M. Если фирма выделила j-й радиостанции уj долларов, то число рекламных объявлений будет Kj(yj) (Kj - функция, которая каждой выделенной сумме ставит в соответствие количество рекламных объявлений в день, считается известной). Как нужно финансировать s радиостанций, чтобы получить суммарную максимальную прибыль от реакции сбыта на рекламу ?
Очевидно, что математическая модель имеет вид:
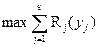
при ограничениях
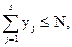

yj ³ 0, j = 1,…,s.
Пример 6. (Задача управления производством). Фирма должна разработать календарную программу выпуска некоторого вида изделий на плановый период, состоящий из Т отрезков (недель, месяцев, кварталов, лет). Предполагается, что для каждого из этих отрезков имеется точный прогноз спроса на выпускаемую продукцию. Время изготовления партии изделий настолько мало, что им можно пренебречь. Для разных отрезков спрос неодинаков; кроме того, на экономические показатели производства влияют размеры изготовляемых партий. Хранение возникающих при этом запасов (превышение выпуска над спросом на некоторых отрезках) связано с определенными затратами.
Требуется разработать такую программу, при которой общая сумма затрат на производство и содержание запасов минимальна при условии полного удовлетворения спроса на продукцию.
Обозначим:
xt - выпуск продукции в течение некоторого отрезка t;
yt - уровень запасов на конец отрезка t;
Dt - спрос на продукцию для отрезка t;
Затраты на отрезке t (обозначим их Сt) зависят от выпуска xt и уровня запасов yt, т.е. являются функцией от неизвестных величин: ct = ct (xt, yt).
Требование удовлетворения спроса в пределах каждого временного отрезка означает, что уровень запасов на конец отрезка t (т.е. yt) должен равняться сумме - уровня запасов на начало отрезка t (т.е. yt-1) и выпуска продукция на отрезке t (т.е. xt) минус спрос на отрезке t (т.е. Dt).
Отсюда получаем следующую модель:
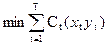
при ограничениях
уt-1 + xt - yt = Dt, t=1,2,…T;
yT = 0, xt, yt ³ 0 для всех t.
Здесь y0 - заданный уровень запасов на начало планового периода, а yT -уровень запаса на конец периода.
Пример 7.(Оптимизация схемы обслуживания). Система обслуживания состоит из n типов различных приборов (напр. кассы в магазинах, телефонные линии, автозаправочные колонки и пр.). Каждый прибор в любой момент времени обслуживает не более одной заявки (напр. покупателя, телефонного разговора, автомобиля и пр.). Известно количество приборов j-го типа и число заявок i-го типа, прибывших в систему в момент времени t. Известна также эффективность j-го прибора при обслуживании заявки i-го вида.
Требуется распределить свободные приборы по заявкам так, чтобы суммарная эффективность была наибольшей.
Для составления модели сначала введем обозначения свободных величин:
Nj - количество приборов j-го типа,
dit - число заявокi-го типа в момент времени t.
μij - эффективность j-го прибора при обслуживании заявки i-го вида. Обозначим искомую величину:
xij- число приборов j-го вида, отведенных для обслуживания заявок i-го типа.
Этих данных достаточно для составления математической модели задачи:
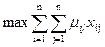
при ограничениях
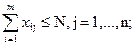
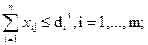
xij - целые неотрицательные числа для всехi, j, здесь m и n заданные числа видов заявок и приборов.
Пример 8. (Выбор оптимального вида посевной культуры). Фермер может посеять одну из трех культур: A1, А2 или А3. Урожаи этих культур во многом зависят от погоды. Требуется установить, какую из этих культур сеять, чтобы обеспечить наибольший доход, если известны цена аi одного центнера культуры Ai, i = 1,2,3, и средняя урожайность каждой культуры в зависимости от погоды (будет ли лето засушливым нормальным или дождливым). Достоверный прогноз погоды отсутствует.
Обозначим через hij - урожайность i-й культуры при погодных условиях j (здесь j=1 - обозначение засушливого лета, j=2 - нормального лета, j=3 – дождливого лета). Числа hij, как и числа ai, заданы (известны). Реально может иметь место только одна из ситуаций (i,j), i = l, 2, 3; j = l, 2, 3. Причем (i,j) означает, что посеяна культура Aj, а погода находится в состоянии j. Всего таких ситуаций девять. JIПР (фермер) может выбрать только вид культуры, состояние погоды от него не зависит.
Если фермер засеял культуру A1, то он может получить (в зависимости от состояния погоды) один из следующих доходов:
a1h11, a1h12, a1h13
соответственно для культуры A2 :
a2h21, a2h22, a2h23
и для культуры А3:
a3h31, a3h32, a3h33
Напишем все эти исходы в одну таблицу (матрицу):
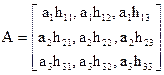
Эта матрица и есть математическая модель исходной задачи. В ней действие фермера сводится к выбору одной из строк матрицы (одной из трех стратегий). Его доход зависит от "выбора" природой одного из своих состояний (одного из трех столбцов матрицы). Например, если фермер посеял культуру A2, а лето получилось дождливым, то доход фермера равен a2h23.
Пример 9. (Выбор ассортимента товаров). На базе торговой организации имеется n типов одного из товаров ассортиментного минимума. В магазин должен быть завезен только один из типов данного товара. Требуется выбрать тот тип товара, который целесообразно завести в магазин. Если товар типа j будет пользоваться спросом, то магазин от его реализации получит прибыль pj, если же он не будет пользоваться спросом - убыток qj.
Составить математическую модель этой задачи в условиях неопределенного покупательского спроса.
Руководствуясь формализацией задачи примера 8, обоснуйте, что искомая модель имеет вид:
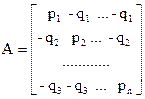
Объясните задачу магазина на этой модели.
Пример 10.(Планирование оптимального срока окончания проекта). Компания должна реализовать проект строительства объекта, состоящий из nопераций (работ). Руководители комплекса оценили продолжительность выполнения каждой операции и установили последовательность операций, т.е. точно определили, какие операции обязательно должны быть закончены, чтобы могла начаться любая из операций, входящих в комплекс.
Руководству компании нужно выяснить, какова наименьшая возможная продолжительность реализации всего проекта, т.е. наиболее ранний из всех возможных сроков его завершения.
При составлении математической модели предположим (для простоты), что проект состоит из пяти операция А,В,С,Д,Е. По условию задачи известны последовательность операций и их продолжительность. Пусть эти данные для наших пяти операций таковы:
| операции | непосредственно предшествующие операции | продолжительности операций |
| А | - | tA |
| В | - | tB |
| С | А | tC |
| D | А | tD |
| Е | B,D | tE |
| F | С,Е | - |
Фиктивная операция F, начинающаяся в момент завершения проекта, вводится для удобства (см. ниже). Второй столбик таблицы означает, что операцию С нельзя начать, прежде чем незакончена операция А и т.д.
Примем, что переменными являются сроки начала операции (введем лишь те из них, которые нужны для решения задачи):
yCD - момент начала операций С и Д;
yE - момент начала операции Е;
yF - момент начала операции F.
Здесь, yF на самом деле есть момент завершения всего комплекса. Моменты yA и yB - это моменты 0 начала операций, т.к. операции А и В не имеют предшествующих. Модель имеет вид:
min yF
при ограничениях
yCD ≥ tA
yE ≥ tB
yE ≥ tD + yCD
yF ≥ tC + yCD
yF ≥ tE + yE
Тесты
1. Что является объектом и языком исследования в экономико-математическом моделировании:
а) различные типы производственного оборудования и методы его конструирования;
б) экономические процессы и специальные математические методы;
в) компьютерные программы и языки программирования.
2. Какое из утверждений верно:
а) экономико-математическая модель – это образ реального объекта в материальной или идеальной форме, отражающей существенные свойства моделируемого объекта и замещающий его в ходе исследования;
б) экономико-математическая модель – это математическое описание экономического процесса, произведенное в целях его исследования;
в) экономико-математическая модель – это математическое описание экономического процесса, необходимое для доказательства гипотез экономической теории.
3. В основе классификации экономико-математических моделей по содержательной проблеме лежит:
а) объект моделирования;
б) цель моделирования;
в) специальный программный комплекс.
4. Методологическое и методическое обоснование модели предполагает:
а) формализацию экономической проблемы;
б) изучение особенностей объекта моделирования и их отражение с помощью структуры разрабатываемой модели;
в) экспериментальные расчеты.
5. Что понимается под термином “исследование операций”?
а) применение математических методов для обоснования решений;
б) применение количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности, в том числе и в экономике;
в) применение математических методов для исследования бухгалтерских операций;
г) содержимое а и б пунктов;
д) содержимое а, б и в пунктов.
6. Когда впервые появился термин “исследование операций”?
а) в годы второй мировой войны;
б) в 50-ые годы;
в) в 60-ые годы;
г) в 70-ые годы;
д) в 90-ые годы.
7. Назовите примеры отраслей производственной сферы, в которых легко просматриваются характерные особенности задач исследования операций в экономике?
а) постройка участка магистрали;
б) продажа сезонных товаров;
в) снегозащита дорог;
г) выборочный контроль продукции;
д) все вышеназванное.
8. Какие решения называются оптимальными?
а) решения, по тем или иным признакам предпочтительные перед другими;
б) рациональные решения;
в) все согласованные решения;
г) все утвержденные решения;
д) все вышеназванные.
9. В чем заключается цель исследования операций?
а) предварительное количественное обоснование оптимальных решений;
б) указать одно-единственное строго оптимальное решение;
в) выделить область практически равноценных оптимальных решений, в пределах которой может быть сделан окончательный выбор;
г) содержимое пунктов а, б, в;
д) только содержимое пунктов а, б.
10. Что необходимо для того, чтобы сравнить между собой по эффективности разные решения?
а) нужно иметь какой-то количественный критерий, так называемый показатель эффективности;
б) нужно иметь целевую функцию;
в) показатель, отражающий целевую направленность операции;
г) содержимое пунктов а, б, в;
д) содержимое пунктов а, б.
Ответы к тестам
| 1) б | 6) г |
| 2) б | 7) б |
| 3) а | 8) а |
| 4) б | 9) г |
| 5) в | 10) г |
Контрольные вопросы
1. Привести классификацию экономических моделей.
2. Сущность и значимость экономико-математического моделирования.
3. Этапы экономико-математического моделирования.
4. Область применения экономико-математических моделей.
5. Экономическая значимость каждого этапа моделирования.
6. Сущность критерия практики.
7. Обязательные элементы математической модели.
8. Что такое оптимальное решение?
| <== предыдущая страница | | | следующая страница ==> |
| Основные типы экономических моделей | | | Задания и задачи. 1. Для рытья котлована объемом 1080 м3 строители получили три экскаватора |
Дата добавления: 2015-07-26; просмотров: 220; Нарушение авторских прав

Мы поможем в написании ваших работ!