Interquartile range for grouped data

Date: 2015-10-07; view: 425.

Suppose that a class, with lower boundary L and upper boundary U, contains f observations. If these observations were to be arranged in ascending order, the observation is estimated by

for

where

is the lower limit of class containing observation

is the upper limit of class containing observation

is the frequency of class containing observation

is the location of observation in that class.

For interquartile range we need to find

and

As we know .

Example: The following table gives the frequency distribution of the number of orders received each day during the past 50 days at the office of a mail-order company

Calculate the interquartile range.

Solution:

First of all, let us write cumulative frequency distribution

Number of orders		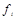Cumulative frequency
10-12 13-15 16-18 19-21

Since there are N=50 observations, we have

Hence the first quartile is the three-quarters way from the observation to 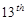. From cumulative distribution we see that the value is the value in the class 13-15. In our notation then

;

The observation is estimated by

Similarly, the 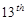observation is the 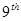value in the same class, so now, with , we have

=

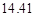
Since the first quartile is three-quarters of the way from the twelves observation to the thirteens observation, we have

.

To find third quartile, we have

Therefore, when the observations are arranged in ascending order, the third quartile is half of the way from thirty-seventh to thirty-eighth.

Looking at table, we see that the thirty-seventh observation is the first value in class the 19-21, which contains t14 observations. We have then

;

Thus, the thirty-seventh observation us estimated by

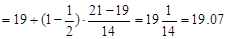
Similarly, the thirty-eighth observations the second value in the same class, so with , we estimate observation by

Hence, since the third quartile is half of the way from the to ,

we have

Finally, then the interquartile range is the difference between the third and first quartiles, so

Interquartile range=

Thus, if the interquartile range is to be used as a measure of dispersion, we estimate it by .