Вычисление определителей при помощи разложения по строке (столбцу). Транспонирование матрицы. Линейная комбинация строк матрицы. Свойства определителя.

Date: 2015-10-07; view: 586.

Вычисление определителя матрицы порядка n сводится к вычислению n определителей различных матриц порядка n-1 с использованием метода разложения по строке (столбцу).

Рис.2

Рассмотрим элемент матрицы (элемент, стоящий на пересечении строки i и столбца j). На Рис. 2 изображена матрица, знаки в которой чередуются по закону (знаки чередуются в шахматном порядке). Минором элемента называется определитель матрицы, образованного вычёркиванием строки i и столбца j из исходной матрицы. Алгебраическое дополнение 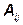элемента матрицы вычисляется по формуле . Имеет место следующее разложение определителя d по строке i

, или

.

Определитель d может быть так же вычислен при помощи разложения определителя d по строке j

, или

.

Пример 3. Вычислить определитель матрицы .

Решение. Для разложения удобно выбрать четвёртую строку, поскольку она содержит много нулей. Пользуясь формулой разложения определителя по строке, получим сумму, каждое слагаемое в которой, представляет собой произведение элемента матрицы B, минора этого элемента матрицы, взятого со знаком элемента, стоящего в том же месте в матрице на Рис. 2.

.

.

.

2.1 Вычислите определители четвёртого порядка методом разложения по строке (столбцу).

1. 2. 3. 4.

Будем говорить, что строка i определителя есть линейная комбинация его остальных строк, если для всякой строки с номером j , j=1, …, i-1, i+1, …, n, можно указать такое число , что, умножая строку j на , а затем складывая все строки, кроме строки i ( причём сложение строк следует понимать так, что складываются элементы всех этих строк в каждом столбце отдельно), получаем строку i.

Транспонирование матрицы- это преобразование, переводящее матрицу в транспонированную матрицу . При этом строки исходной матрицы становятся столбцами транспонированной.

Пример 4. . Решение. Получаем .

Свойства определителя:

· Определитель не меняется при транспонировании.

· Если одна из строк определителя равна нулю, то определитель равен нулю.

· При перестановке двух строк, определитель меняет знак.

· Определитель, содержащий две одинаковые строки, равен нулю.

· Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.

· Определитель, содержащий две пропорциональные строки, равен нулю.

· Если все элементы некоторой (одной) строки представлены в виде суммы , то

= + .

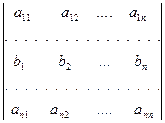· Если одна из строк есть линейная комбинация его других строк, то определитель равен нулю.

· Определитель не меняется, если к элементам одной из его строк прибавляются соответственные элементы другой строки, умноженные на одно и то же число.

2.2 Пользуясь свойствами определителей укажите, какие определители из упражнения 1.2 равны нулю и почему?