Операции над матрицами (сложение, умножение, умножение на число, транспонирование). Решение системы линейных уравнений правилом Крамера.

Date: 2015-10-07; view: 433.

Суммой А+В двух квадратных матриц и порядка n называется матрица , всякий элемент которой равен сумме соответствующих элементов матриц А и В; .

Разностью А-В двух квадратных матриц и порядка n называется матрица , всякий элемент которой равен сумме соответствующих элементов матриц А и В; .

Произведением kA квадратной матрицы на число k, называется матрица , получающаяся умножением на k всех элементов матрицы A.

Умножение матриц AB=С, где определено, если число столбцов матрицы А равно числу строк матрицы В. При этом строки матрицы А умножаются на столбцы матрицы В. Если строка i матрицы А умножается на столбец j матрицы В, то результатом будет элемент .

Пример 5. , . Вычислите AB.

Решение. .

Транспонированием матрицы называется преобразование, переводящее матрицу A в матрицу . Матрица называется транспонированной матрицей.

3.1 , . Вычислите

1. 2. 3. 4. 5. 6.

7. 8. 9. 10.

Решение системы линейных уравнений порядка n можно записать при помощи правила Крамера (i=1, 2, …, n), где – определитель матрицы A, – определитель матрицы, образованной из матрицы A заменой столбца j на столбец свободных членов В.

Если и для некоторого j , то система линейных уравнений решений не имеет (Решением будет пустое множество).

Если и для всех j , то система линейных уравнений имеет либо бесконечное множество решений либо решений не имеет.

Правило Крамера можно использовать для решения системы линейных уравнений третьего порядка

Рассмотрим определители:

, , , .

Значения переменных 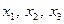равны

, , .

3.2 Решите, пользуясь правилом Крамера, системы линейных уравнений второго порядка, проверив результат подстановкой полученных значений в системы.

1. 2. 3. 4.