Решение системы линейных уравнений при помощи метода Гаусса. Теорема Кронекера- Капелли.

Date: 2015-10-07; view: 541.

Систему линейных уравнений

можно записать в виде расширенной матрицы

Матрицу называют матрицей коэффициентов.

Система линейных уравнений называется совместной, если она имеет решения.

Теорема 4.1 Кронекера-Капелли.Система линейных уравнений тогда и только тогда совместна, когда ранг расширенной матрицы равен рангу матрицы коэффициентов.

Рассмотрим следующие элементарные преобразования строк матрицы

· Любые две строки можно менять местами.

· Любую строку можно разделить (или умножить) на некоторое не нулевое число.

· Строку i можно прибавить к другой строке j (отнять из строки j) и результат записать вместо строки j. При этом складываются (вычитаются) элементы, стоящие в одном и том же столбце.

· Любую строку можно разделить (или умножить) на некоторое не нулевое число, получившуюся строку отнять из некоторой другой строки j и результат записать вместо этой строки j.

Пользуясь этими преобразованиями, матрицу можно привести к верхнетреугольному виду.

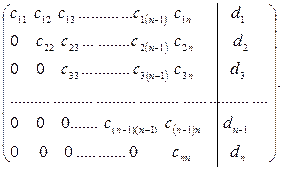
Для этого

· Если , то первую строку матрицы умножаем на и вычитаем из второй строки, записав результат вместо второй строки, затем первую строку матрицы умножаем на и вычитаем из третьей строки, записав результат вместо третьей строки, и т.д. При этом все элементы в первом столбце, кроме элемента в первой строке и первом столбце будут нулями.

· Если элемент был равен нулю, то ищем в первом столбце не нулевой элемент, и меняем местами первую строку и строку, с этим не нулевым элементом и переходим к предыдущему пункту.

· Аналогично преобразовываем второй столбец и т. д.

Матрицу в верхнетреугольном виде можно записать в виде системы линейных уравнений, решение которой легко находится.

Пример 6.Решить систему

Решение. Подвергаем преобразованиям расширенную матрицу этой системы

Мы приходим, следовательно, к системе уравнений

, обладающей единственным решением .

4.1 Решите, пользуясь правилом Крамера и методом Гаусса, системы линейных уравнений третьего порядка, проверив результат подстановкой полученных значений в системы.

1. 2. 3. 4.