Единичная матрица. Операции над матрицами. Вычисление обратной матрицы.

Date: 2015-10-07; view: 448.

Матрица E= .

называется единичной матрицей.

Для суммы и произведения матриц справедливы следующие соотношения:

· ,

· ,

· ,

· ,

· ,

где Е–единичная матрица.

5.1 Приведите пример, который показывает, что в общем случае .

Теорема 5.1.Если определитель квадратной матрицы А не равен нулю, то можно найти такую матрицу , для которой выполнено равенство . Матрица называется обратной матрицей к матрице .

Первый способ вычисления обратной матрицы (метод Гаусса).Рассмотрим матрицу

A= .

К матрице справа допишем единичную матрицу

Пользуясь элементарными преобразованиями строк матрицы, описанных в предыдущем параграфе, расширенную матрицу можно привести к виду.

Матрица , записанная справа от черты будет обратной к матрице А.

Второй способ вычисления обратной матрицы.Пусть определитель матрицы А, и алгебраическое дополнение элемента матрицы А, тогда обратная матрица записывается в виде:

= .

Схема вычисления обратной матрицы включает следующие 5 шагов:

1. Вычисляется определитель матрицы А. Если определитель , то обратной матрицы не существует.

2. Находится матрица миноров.

3. Находится матрица алгебраических дополнений.

4. Матрица алгебраических дополнений транспонируется.

5. Каждый элемент транспонированной матрицы алгебраических дополнений делится на .

Пример 7. Вычисление обратной матрицы к матрице

Решение

1. Определитель .

2. Матрица миноров .

3. Матрица алгебраических дополнений .

4. Транспонирование .

5. Деление на определитель .

6. Проверка умножением матриц

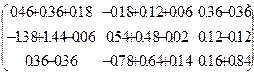* = =E,

где -единичная матрица.

Пример 8.Вычисление обратной матрицы к матрице .

Решение.

1. Определитель .

2. Матрица миноров .

3. Матрица алгебраических дополнений .

4. Транспонирование .

5. Деление на определитель .

6. Проверка .

5.1 Вычислите обратную матрицу, проверив результат умножением исходной матрицы на обратную.

1. 2. 3. 4. 5.