Определители высших порядков.

Date: 2015-10-07; view: 390.

Пусть дана матрица n-го порядка

A=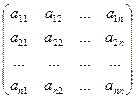

Определителем этой матрицы называется число, полученное по следующему правилу:

det(A)=a₁₁A₁₁+a₁₂A₁₂+a₁₃A₁₃+…+a_1nA_1n (2),

причем A_ij=(-1)^i+jM_ij, а минор M_ij будет определителем матрицы (n-1)-го порядка.

Формула (2) есть разложение определителя по элементам первой строки.

Все свойства (10 штук) верны для матриц n-го порядка.

Проверим, например, свойство 3^°.

3^° - если матрица имеет две одинаковые строки (или столбца), то определитель этой матрицы равен нулю.

Доказательство: пусть в матрице A совпадают i-е и k-е строки. Переставим в этой матрице i-ую строку на место k-ой и обратно. Так как строки одинаковы, то ни сама матрица, ни ее определитель не изменяются, но вместе с тем при перестановке в матрице двух любых строк определитель матрицы изменит свой знак, то есть det(A)=-det(A), а это возможно, только, если det(A)=0.

Свойство 4^° - если все элементы какой-либо строки (столбца) умножить на одно и то же число, то определитель окажется умноженным на то же число.

Рассмотрим матрицы

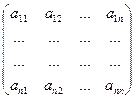A= и A^/=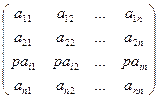

Разлагая определители этих матриц по элементам i-ой строк, получим

det(A)=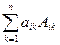

det(A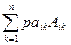^/)= =p×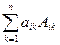

Итак, det(A^/)=p×det(A).