Матрицы.

Date: 2015-10-07; view: 415.

Линейная алгебра.Матрицы. Действия над ними.

ЛЕКЦИЯ N7.

1. Матрицы. 28

2.Умножение матриц. 30

3.Основные свойства действия над матрицами. 31

Итак, на предыдущей лекции мы рассматривали матрицы, состоящие из одинакового числа строк и столбцов, то есть квадратные. Число строк и столбцов квадратной матрицы называется ее порядком.

Квадратная матрица n-го порядка имеет вид:

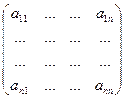
Главной диагональюквадратной матрицы называется диагональ матрицы, составленная из элементов a₁₁, a₂₂, a₃₃,…, a_nn.

Симметрической матрицейназывается квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, равны друг другу, то есть a_ke=a_ek

Пример:

Диагональнойматрицей называется квадратная матрица, у которой все элементы, не находящиеся на главной диагонали, равны нулю - .

Треугольной (наддиагональной)называется квадратная матрица, если из i>k следует a_ik=0.

Мономиальнойназывается квадратная матрица, в каждой строке и в каждом столбце которой стоит лишь один элемент, отличный от нуля.

Единичнойназывается диагональная матрица, у которой каждый элемент, находящийся на главной диагонали, равен единице- Е = .

Нулевойматрицей называется матрица, у которой все элементы равны нулю и обозначают 0 или 0_mn.

Следомквадратной матрицы А называется сумма ее диагональных элементов.

Матрицы могут быть и прямоугольными, имеющими k строк и l столбцов, например,

Матрица, имеющая только одну строку, называется матрицей-строкой, например, , а матрица, имеющая только один столбец, называют матрицей-столбцом, например:

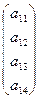
Матрицы A и B называются равными, если они имеют одно и то же число строк и одно и то же число столбцов (то есть, если они одного размера) и если при этом каждый элемент a_kl матрицы A равен соответствующему элементу b_kl матрицы B.

A= ; B=

A=B

Суммойматриц A и B, имеющих одинаковое число строк и столбцов

A= ; B=

называется третья матрица

C=

каждый элемент которой равен сумме соответствующих элементов слагаемых матриц, то есть с_kl=a_kl+b_kl (k=1,2,…,m; l=1,2,…,n).

Сумма матриц обозначается так C=A+B.

Аналогично определяется разность матриц:

C=A-B, где c_kl=a_kl-b_kl

Пример: A= ; B= ; C= ; где С=А+В

Произведение числа λ на матрицу A называется матрица, определяемая равенством:

λ× = 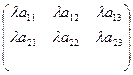и получаемая из A умножением всех ее элементов на λ. Обозначается B=λA.