Обратная матрица.

Date: 2015-10-07; view: 392.

Ранг матрицы. Собственные векторы и собственные значения.

Обратная и ортогональная матрицы.

ЛЕКЦИЯ N8.

1.Обратная матрица. 32

2.Ранг матрицы. Эквивалентные матрицы. 34

3.Элементарные преобразования матрицы. 34

4.Собственные числа и собственные векторы матрицы. 35

Определение:Если определитель квадратной матрицы отличен от нуля, то матрица

называется невырожденной. Если же определитель матрицы равен нулю, то матрица называется вырожденной.

Для квадратных матриц введем понятие обратной матрицы. Если А – квадратная

матрица, то обратной для нее матрицей называется матрица, обозначаемая А^-1 и

удовлетворяющая условию AA^-1=E (1)

Можно доказать, что А^-1А=Е тоже (2)

Теорема:для того, чтобы квадратная матрица А имела обратную, необходимо и

достаточно, чтобы матрица А была невырожденной, то есть чтобы det(A)≠0.

Доказательство. Необходимость:

предположим, что для матрицы А существует обратная матрица А^-1. Докажем, что в этом случае матрица А должна быть невырожденной, то есть ее определитель ≠0.

Допустим, что |А|=0, тогда |АА^-1|=|А|×|А^-1|=0

Но в силу (1) имеем :

|АА^-1|=|Е|=1, что противоречит предыдущему равенству; Значит, ½А½¹ 0.

Достаточность:

приведем доказательство для матрицы 3-го порядка. Пусть A= - невырожденная матрица, то есть det(A)≠0.

Покажем, что в этом случае существует обратная матрица.

Пусть A_ik – алгебраическое дополнение элемента a_ik.

Матрица А^-1, обратная А получается следующим образом:

1) Составим матрицу В, заменяя в матрице А каждый элемент a_ik его алгебраическим дополнением A_ik, деленным на определитель |А| матрицы А:

В=

2) Составим матрицу В^*, как транспонированную к В

В^*=

Докажем, что В^* является обратной А.

Для этого составим произведение:

АВ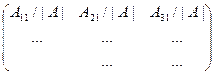^*= = = =Е.

Итак, АВ^*=Е, поэтому В^*=А^-1.

А^-1= и, следовательно, обратная матрица существует.

Пример: А= ; |А|=-9; А₁₁=3; А₁₂=-6; А₁₃=3; А₂₁=-4; А₂₂=2; А₂₃=-1; А₃₁=2; А₃₂=-1; А₃₃=-4.

В=

А^-1=В^*= .

Докажем, что определители матриц А и А^-1 обратны по величине.

|А^-1|=1/|А|.

Знаем, что АА^-1=Е→|АА^-1|=|А|×|А^-1|=|Е|=1→|А^-1|=1/|А|.

Определение:ортогональной называется матрица А^*, если А^*А=АА^*=Е, то есть, если А^*=А^-1.