Алгоритм нахождения обратной матрицы

Date: 2015-10-07; view: 422.

1.

2. транспонировать матрицу А

3. вычислить алгебраические дополнения всех элементов транспонированной матрицы

4.составляем матрицу А*(союзная или присоединенная)

5.

Пример 12: Найти обратную матрицу для матрицы

А=

Решение: Т.к. определитель равен , то обратная матрица имеет место быть.

Транспонируем матрицу

Вычислим все алгебраические дополнения

транспонированной матрицы

Т.о. союзная матрица имеет вид

Обратная матрица имеет вид .

Замечание:иногда обратную матрицу записывают .

Пример 13: При каких значениях l матрица не имеет обратную?

Решение: Если определитель матрицы равен нулю, то такая матрица не имеет обратной. Нужно вычислить определитель данной матрицы и приравнять его к нулю. Получим уравнение первого порядка, из которого и найдем значение

или следовательно

Пример 14: При каких значениях l матрицы

и перестановочны?

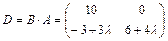
Сравнив матрицы С и D, находим .

Пример 15: Вычислить

Найдем матрицу

Затем найдем матрицу