
Координаты вектора и точки в декартовой системе координат.
Date: 2015-10-07; view: 546.
Декартова прямоугольная система координат является частным случаем аффинной системы.
В случае декартовой прямоугольной системы базисные векторы принято обозначать не буквами a, b, c, а буквами i,j, k.
Итак, каждый из векторов i, j, k имеет длину, равную единице, причем эти три вектора взаимно-ортогональны (обычно направления векторов i, j, k берут совпадающими с направлениями декартовых осей Oх, Oy и Oz соответственно).
Если скалярное произведение двух элементов пространства равно нулю, то они называются ортогональными друг другу.
Каждый вектор d может быть разложен единственным способом по декартову прямоугольному базису i, j, k, т. е. для каждого вектора d найдется единственная тройка чисел X, Y и Z такая, что справедливо равенство:
d = Xi + Yj + Zk.
Числа X, Y, Z называются декартовыми прямоугольными координатами вектора d.
Если вектор d имеет декартовы прямоугольные координаты X, У, Z, то мы будем использовать следующую символику: d={X, Y, Z}.
Декартовы прямоугольные координаты X, Y и Z вектораd равны проекциям этого вектора на оси Oх, Oу
и Oz соответственно.
Возьмем произвольную точку М на прямой a. Декартовой координатой x точки M будем называть величину направленного отрезка 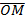 .
.
| <== previous lecture | | | next lecture ==> |
| Разложение вектора по базису. Координатное представление. | | | Длина вектора. Расстояние между двумя точками. Орт вектора. Координаты орта. Косинусы направления. |