Длина вектора. Расстояние между двумя точками. Орт вектора. Координаты орта. Косинусы направления.

Date: 2015-10-07; view: 492.

Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора. Для обозначения модуля вектора используются две вертикальные линии слева и справа | |.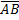

Величина М₁М₂ направленного отрезка М₁М₂ равна x₂ — х₁ т. е. М₁М₂ = х₂-х₁.

Рассмотрим в пространстве декартову систему координат Oxyz и точки M1(x1,y1,z1) и М2{х2, у2, z2) Расстояние ρ(М₁, М₂) между точками М₁ и М₂, равное длине направленного отрезка 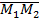, равно также длине диагонали параллелепипеда, грани которого параллельны координатным плоскостям и проходят через точки М₁ и М₂. Длина параллельного оси Ох ребра этого параллелепипеда равна, абсолютной величине проекции отрезка М₁М₂ на ось Ох, т. е., согласно формуле равна |x₁ —x₂|. По аналогичным соображениям длины ребер, параллельных осям Оу и Oz, равны соответственно |y₂ — y₁| и |z₂ — z₁|.

Используя теорему Пифагора, получим следующую формулу для ρ(М₁, М₂):

ρ(М₁, М₂) =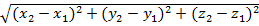

Формула расстояния между двумя точками в случае их расположения в плоскости Оху имеет следующий вид:

ρ(М₁, М₂) =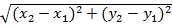

Ортом произвольного ненулевого вектора c назовем единичный вектор, коллинеарный c и имеющий одинаковое с c направление.

Координаты орта - координаты a⁰( 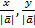), где a⁰ орт вектор.

Косинусы направления вектора - это косинусы углов, которые образует вектор с осями координат.